题目内容
已知函数
(1)当 时,求
时,求 的值域;
的值域;
(2)当 ,
, 时,函数
时,函数 的图象关于
的图象关于 对称,求函数
对称,求函数 的对称轴。
的对称轴。
(3)若 图象上有一个最低点
图象上有一个最低点 ,如果图象上每点纵坐标不变,横坐标缩短到原来的
,如果图象上每点纵坐标不变,横坐标缩短到原来的 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得 的图象,又知
的图象,又知 的所有正根从小到大依次为
的所有正根从小到大依次为 ,且
,且 ,求
,求 的解析式。
的解析式。
【答案】
(1)当 时,
时,
当 时,值域为:
时,值域为:
当 时,值域为:
时,值域为:
(或将 分三类讨论也行)
分三类讨论也行)
(2)当 ,
, 时,
时, 且图象关于
且图象关于 对称。
对称。
∴


∴函数 即:
即:
∴ 由
由 [来源:ZXXK]
[来源:ZXXK]
∴函数的对称轴为:
(3)由

(其中 ,
, )
)
由 图象上有一个最低点
图象上有一个最低点 ,所以
,所以
∴ ∴
∴
又图象上每点纵坐标不变,横坐标缩短到原来的 倍,然后向左平移1个单位可得
倍,然后向左平移1个单位可得 的图象,则
的图象,则
又∵ 的所有正根从小到大依次为
的所有正根从小到大依次为 ,且
,且
所以 与直线
与直线 的相邻交点间的距离相等,根据三角函数的图象与性质,直线
的相邻交点间的距离相等,根据三角函数的图象与性质,直线 要么过
要么过 的最高点或最低点,要么是
的最高点或最低点,要么是
即: 或
或 (矛盾)或
(矛盾)或

 或
或
当 时,函数的
时,函数的 

直线 和
和 相交,且
相交,且 ,周期为3(矛盾)
,周期为3(矛盾)
当 时,函数
时,函数 

直线 和
和 相交,且
相交,且 ,周期为6(满足)
,周期为6(满足)
综上:
【解析】略

练习册系列答案
 出彩同步大试卷系列答案
出彩同步大试卷系列答案
相关题目
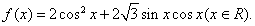
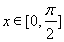
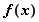

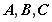
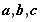
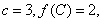
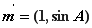
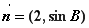
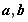

 时,求函数的最大值和最小值;
时,求函数的最大值和最小值; 的取值范围,使
的取值范围,使 在区间
在区间 上是单调减函数
上是单调减函数 .(
.( ).
). 时,求函数
时,求函数 的极值;
的极值; (2)若对
(2)若对 ,有成立,求实数
,有成立,求实数 的取值范围.
的取值范围.
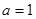 时,求
时,求 的极小值;
的极小值; ,求
,求 的最大值
的最大值 .
.