题目内容
已知△AOB,O为坐标原点,点A(1,0),B为椭圆
+y2=1上的动点,若点M满足
=
+
求点M的轨迹方程.
| x2 |
| 4 |
| OM |
| 2 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
分析:设点M的坐标为(x,y),因为点M随着点B在动,故设动点B(m,n),则动点B的轨迹为已知,由
=
+
找到点M与点B间的坐标关系,代入椭圆方程即可得点M的轨迹方程
| OM |
| 2 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
解答:解:设M(x,y),B(m,n)
∴
=(x,y),
=(1,0),
=(m,n)
∵
=
+
∴(x,y)=
(1,0)+
(m,n)
∴
即
∵B为椭圆
+y2=1上的动点,
∴
+n2=1
∴
+(3y)2=1
化简得(3x-2)2+36y2=4
∴点M的轨迹方程为(3x-2)2+36y2=4
∴
| OM |
| OA |
| OB |
∵
| OM |
| 2 |
| 3 |
| OA |
| 1 |
| 3 |
| OB |
∴(x,y)=
| 2 |
| 3 |
| 1 |
| 3 |
∴
|
|
∵B为椭圆
| x2 |
| 4 |
∴
| m2 |
| 4 |
∴
| (3x-2)2 |
| 4 |
化简得(3x-2)2+36y2=4
∴点M的轨迹方程为(3x-2)2+36y2=4
点评:本题考查了解析几何的基本思想,坐标法求动点的轨迹方程,向量与解析几何的综合

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 ,则向量
,则向量  +y2=1上的动点,若点M满足
+y2=1上的动点,若点M满足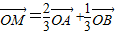 求点M的轨迹方程.
求点M的轨迹方程.