题目内容
已知函数f（x）=
，方程f2（x）+mf（x）=0有五个不同的实数解时，m的取值范围为 ．
|
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：作出函数f（x）的图象，根据方程f2（x）+mf（x）=0有五个不同的实数解时，等价f（x）=0或f（x）=-a，利用数形结合即可得到结论．
解答：
解：作出函数f（x）的图象如图：由图象可知当f（x）=0时，方程有两个根，
当f（x）＞3时，函数f（x）=y有两个不同的交点，
由f2（x）+mf（x）=0，得f（x）[f（x）+m]=0，
要使方程f2（x）+mf（x）=0有五个不同的实数解，
则等价为f（x）+m=0，即f（x）=-m有三个不同的实数解，
此时0＜-m≤3，
即-3≤m＜0，
故答案为：[-3，0）
解：作出函数f（x）的图象如图：由图象可知当f（x）=0时，方程有两个根，当f（x）＞3时，函数f（x）=y有两个不同的交点，
由f2（x）+mf（x）=0，得f（x）[f（x）+m]=0，
要使方程f2（x）+mf（x）=0有五个不同的实数解，
则等价为f（x）+m=0，即f（x）=-m有三个不同的实数解，
此时0＜-m≤3，
即-3≤m＜0，
故答案为：[-3，0）
点评：本题主要考查函数零点个数的应用，作出函数f（x）的图象，利用数形结合是解决本题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）=2cosxsin（x+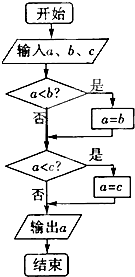
阅读如图的算法流程图：若a=sin60°，b=cos60°，c=tan60°，则输出的应该是