题目内容

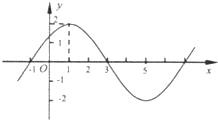
函数f(x)=Asin(ωx+φ)+B(A＞0，ω＞0，|φ|＜
π
2
)的图象上一个最高点的坐标为(
π
12
，3)，与之相邻的一个最低点的坐标为(
7π
12
，-1)．
（Ⅰ）求f（x）的表达式；
（Ⅱ）求f（x）在x=
π
6
处的切线方程．
（Ⅰ）依题意，得
T
2
=
7π
12
-
π
12
=
π
2
，所以T=π，
∴ω=
2π
T
=2…（1分）
又∵
A+B=3
-A+B=-1
，∴解之得
A=2
B=1
…（3分）
再把(
π
12
，3)代入f（x）=2sin（2x+φ）+1，
可得sin(
π
6
+?)=1，所以
π
6
+?=2kπ+
π
2
（k∈Z），
所以?=2kπ+
π
3
，
因为|?|＜
π
2
，所以取k=0得?=
π
3
…（5分）
综上所述，f（x）的表达式为：f(x)=2sin(2x+
π
3
)+1…（6分）
（Ⅱ）因为f（x）的导数为f′(x)=4cos(2x+
π
3
)…（8分）
∴所求切线的斜率k=f′(
π
6
)=4cos(2×
π
6
+
π
3
)=4cos
2π
3
=-2…（9分）
而f(
π
6
)=2sin(2×
π
6
+
π
3
)+1=2sin
2π
3
+1=
3
+1…（10分）
∴f（x）在x=
π
6
处的切线方程为y-(
3
+1)=-2(x-
π
6
)
化简，得6x+3y-3
3
-3-π=0…（12分）
练习册系列答案
相关题目
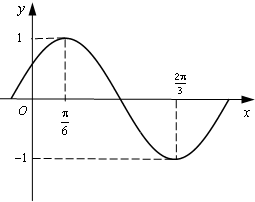精英家教网已知函数f(x)=Asin(ωx+φ)，(A＞0，ω＞0，|φ|＜
π2
，x∈R)的图象的一部分如图所示，则函数f（x）的解析式为
 
．
精英家教网函数f(x)=Asin(ωx+?) (A＞0，ω＞0，|?|＜
π
2
)部分图象如图所示．
（Ⅰ）求f（x）的最小正周期及解析式；
（Ⅱ）设g（x）=f（x）-cos2x，求函数g（x）在区间x∈[0，
π
2
]上的最大值和最小值．
已知函数f(x)=Asin(ωx+?)，x∈R，(A＞0．ω＞0，0＜?＜
π
2
)的图象与x轴的交点中，相邻两个交点之间的距离为
π
2
，且图象上一个最低点为M(
2π
3
，-2)．
（1）求f（x）的解析式；
（2）设A，B，C是△ABC的三个内角，若cosB=
1
3
，f(
C
2
)=
3
，求sinA．
函数f(x)=Asin(ωx-
π
6
)（A＞0，ω＞0）的最大值为2，其最小正周期为π．
（1）求函数f（x）的解析式；
（2）设α∈(0，
π
2
)，则f(
α
2
)=
2
，求cosα的值．
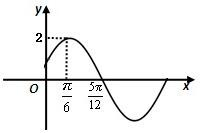（2010•广东模拟）已知函数f(x)=Asin(ωx+φ)(A＞0，ω＞0，|φ|＜
π
2
)的部分图象如图所示．
（1）求函数f（x）的解析式；
（2）令g(x)=f(x+
π
12
)，判断函数g（x）的奇偶性，并说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网