题目内容
已知点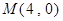 、
、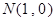 ,若动点
,若动点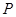 满足
满足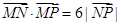 .
.
(1)求动点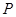 的轨迹曲线
的轨迹曲线 的方程;
的方程;
(2)在曲线 上求一点
上求一点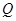 ,使点
,使点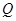 到直线:
到直线: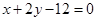 的距离最小.
的距离最小.
(1)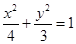 ;(2)
;(2)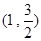 .
.
解析试题分析:本题考查计算能力和参数方程在求圆锥曲线最值中的应用.(1)由向量的坐标运算,模公式可列出式子,化简求解;(2)将椭圆方程化为参数方程,由点到直线的距离公式,转化为求三角函数的最值.
试题解析:(1)设点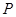 坐标为
坐标为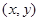 ,则
,则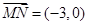 ,
,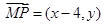 ,
,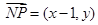 ,
,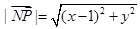 .
.
因为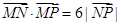 ,所以
,所以 ,化简得
,化简得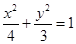 .
.
所以动点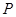 的轨迹为
的轨迹为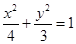 .
.
(2)点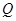 在
在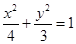 上,设点
上,设点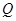 坐标为
坐标为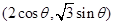 ,
,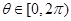 .
.
记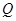 到直线
到直线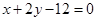 的距离为
的距离为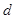
 ,
,
当 时
时 有最小值
有最小值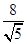 ,
,
此时点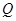 坐标为
坐标为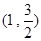 .
.
考点:1、平面向量的坐标运算;2、椭圆方程及其性质;3、点到直线的距离公式;4、椭圆的参数方程;5、三角恒等变换与三角函数运算.

练习册系列答案
相关题目
 :
:
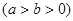 ,
,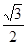 ,求椭圆的标准方程;
,求椭圆的标准方程;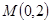 的直线
的直线 与椭圆
与椭圆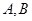 ,且
,且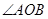 为锐角(
为锐角( 为坐标原点),求直线
为坐标原点),求直线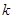 的取值范围;
的取值范围;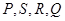 四点,设原点
四点,设原点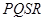 的一边距离为
的一边距离为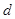 ,试求
,试求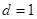 时
时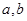 满足的条件.
满足的条件.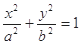 (
(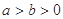 )右顶点到右焦点的距离为
)右顶点到右焦点的距离为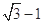 ,短轴长为
,短轴长为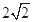 .
.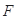 的直线与椭圆分别交于
的直线与椭圆分别交于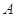 、
、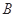 两点,若线段
两点,若线段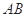 的长为
的长为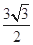 ,求直线
,求直线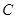 的中心在坐标原点,右准线为
的中心在坐标原点,右准线为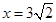 ,离心率为
,离心率为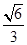 .若直线
.若直线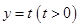 与椭圆
与椭圆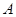 、
、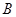 ,以线段
,以线段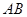 为直径作圆
为直径作圆 .
.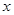 轴相切,求圆
轴相切,求圆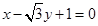 截得的线段长.
截得的线段长. 的左右焦点为F1,F2,离心率为
的左右焦点为F1,F2,离心率为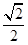 ,以线段F1 F2为直径的圆的面积为
,以线段F1 F2为直径的圆的面积为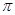 , (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
, (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.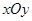 中,已知曲线
中,已知曲线 上任意一点到点
上任意一点到点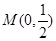 的距离与到直线
的距离与到直线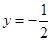 的距离相等.
的距离相等.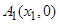 ,
,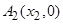 是
是 轴上的两点
轴上的两点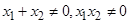 ,过点
,过点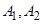 分别作
分别作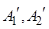 ,直线
,直线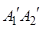 与x轴交于点
与x轴交于点 ,这样就称
,这样就称 确定了
确定了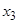 .同样,可由
.同样,可由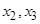 确定了
确定了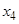 .现已知
.现已知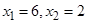 ,求
,求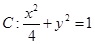 的上、下顶点分别为
的上、下顶点分别为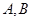 ,点
,点 在椭圆上,且异于点
在椭圆上,且异于点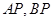 与直线
与直线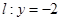 分别交于点
分别交于点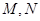 ,
,
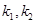 ,求证:
,求证: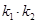 为定值;
为定值;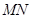 的长的最小值;
的长的最小值;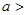
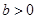 ,曲线
,曲线 上任意一点
上任意一点 分别与点
分别与点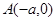 、
、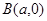 连线的斜率的乘积为
连线的斜率的乘积为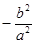 .
.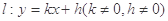 与
与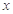 轴、
轴、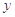 轴分别交于
轴分别交于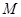 、
、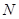 两点,若曲线
两点,若曲线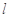 没有公共点,求证:
没有公共点,求证: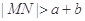 .
.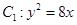 与双曲线
与双曲线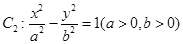 有公共焦点
有公共焦点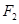 ,点
,点 是曲线
是曲线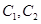 在第一象限的交点,且
在第一象限的交点,且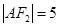 .
.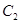 的方程;
的方程; 为圆心的圆
为圆心的圆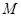 与直线
与直线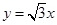 相切,圆
相切,圆 :
: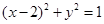 .过点
.过点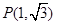 作互相垂直且分别与圆
作互相垂直且分别与圆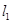 和
和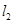 ,设
,设 ,
, ,问:
,问: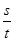 是否为定值?如果是,请求出这个定值;如果不是,请说明理由.
是否为定值?如果是,请求出这个定值;如果不是,请说明理由.