题目内容
5．利用余弦曲线，写出满足cosx＞0，x∈[0，2π]的x的区间是[0，$\frac{π}{2}$）∪（$\frac{3π}{2}$，2π]．分析 画出y=cosx，x∈[0，2π]的图象，数形结合可得cosx＞0，x∈[0，2π]的解集．
解答 解：y=cosx，x∈[0，2π]的图象如下图所示：
由图可得：若cosx＞0，
则x∈[0，$\frac{π}{2}$）∪（$\frac{3π}{2}$，2π]，
故答案为：[0，$\frac{π}{2}$）∪（$\frac{3π}{2}$，2π]
点评 本题考查的知识点是余弦函数的图象和性质，数形结合思想，难度中档．
练习册系列答案
相关题目
20．已知函数f（x）=x2+mx+m+1（m＞5）的两个零点分别为tanα，tanβ，且α，β∈（-$\frac{π}{2}$，$\frac{π}{2}$），则α+β的值为（ ）
| A． | $\frac{π}{4}$ | B． | -$\frac{π}{4}$ | C． | $\frac{3}{4}π$ | D． | -$\frac{3}{4}π$ |
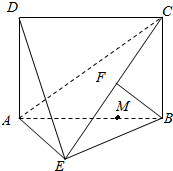如图所示，四边形ABCD为矩形，AD⊥平面ABE，AE=EB=BC，F为CE上的点，且BF⊥平面ACE．