题目内容
设离心率 的椭圆
的椭圆 的左、右焦点分别为F1、F2,P是x轴正半轴上一点,以PF1为直径的圆经过椭圆M短轴端点,且该圆和直线
的左、右焦点分别为F1、F2,P是x轴正半轴上一点,以PF1为直径的圆经过椭圆M短轴端点,且该圆和直线 相切,过点P的直线与椭圆M相交于相异两点A、C.
相切,过点P的直线与椭圆M相交于相异两点A、C.(Ⅰ)求椭圆M的方程;
(Ⅱ)若相异两点A、B关于x轴对称,直线BC交x轴与点Q,求
 的取值范围.
的取值范围.
【答案】分析:(Ⅰ)设以|PF1|为直径的圆经过椭圆M短轴端点N,则|NF1|=a,由 可得a=2c,由此可得
可得a=2c,由此可得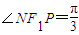 ,再由|PF1|的长可判断F2为圆的圆心,根据圆与直线
,再由|PF1|的长可判断F2为圆的圆心,根据圆与直线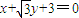 相切,可解得c值,从而可求得a,b;
相切,可解得c值,从而可求得a,b;
(Ⅱ)设点A(x1,y1),C(x2,y2),易知点B(x1,-y1),设直线PA的方程为y=k(x-3),代入椭圆方程消掉y得x的二次方程,由△>0得k2范围,由点斜式写出直线BC的方程,令y=0,由韦达定理可得Q点横坐标,利用向量数量积运算及韦达定理可把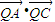 表示为k的函数,由k2的范围即可求得
表示为k的函数,由k2的范围即可求得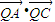 的范围;
的范围;
解答:解:(Ⅰ)设以|PF1|为直径的圆经过椭圆M短轴端点N,
∴|NF1|=a,∵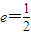 ,∴a=2c,
,∴a=2c,
∴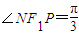 ,|PF1|=2a.
,|PF1|=2a.
∴F2(c,0)是以|PF1|为直径的圆的圆心,
∵该圆和直线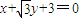 相切,
相切,
∴ ,解得
,解得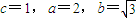 ,
,
∴椭圆M的方程为: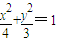 .
.
(Ⅱ)设点A(x1,y1),C(x2,y2),则点B(x1,-y1),
设直线PA的方程为y=k(x-3),
联立方程组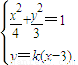 ,消掉y,化简整理得(4k2+3)x2-24k2x+36k2-12=0,
,消掉y,化简整理得(4k2+3)x2-24k2x+36k2-12=0,
由△=(24k2)2-4•(3+4k2)•(36k2-12)>0,得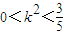 .
.
则 .
.
直线BC的方程为: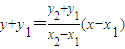 ,
,
令y=0,则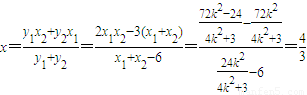 .
.
∴Q点坐标为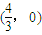 .
.
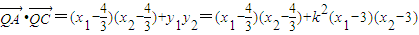
=
=
=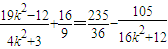 .
.
∵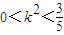 ,
,
∴ .
.
点评:本题考查直线、椭圆方程及其位置关系,考查向量的数量积运算,考查函数思想,考查学生分析解决问题的能力,综合性强,难度较大,对能力要求较高.
 可得a=2c,由此可得
可得a=2c,由此可得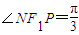 ,再由|PF1|的长可判断F2为圆的圆心,根据圆与直线
,再由|PF1|的长可判断F2为圆的圆心,根据圆与直线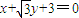 相切,可解得c值,从而可求得a,b;
相切,可解得c值,从而可求得a,b;(Ⅱ)设点A(x1,y1),C(x2,y2),易知点B(x1,-y1),设直线PA的方程为y=k(x-3),代入椭圆方程消掉y得x的二次方程,由△>0得k2范围,由点斜式写出直线BC的方程,令y=0,由韦达定理可得Q点横坐标,利用向量数量积运算及韦达定理可把
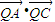 表示为k的函数,由k2的范围即可求得
表示为k的函数,由k2的范围即可求得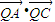 的范围;
的范围;解答:解:(Ⅰ)设以|PF1|为直径的圆经过椭圆M短轴端点N,
∴|NF1|=a,∵
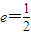 ,∴a=2c,
,∴a=2c,∴
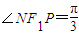 ,|PF1|=2a.
,|PF1|=2a.∴F2(c,0)是以|PF1|为直径的圆的圆心,
∵该圆和直线
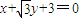 相切,
相切,∴
 ,解得
,解得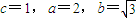 ,
,∴椭圆M的方程为:
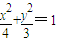 .
.(Ⅱ)设点A(x1,y1),C(x2,y2),则点B(x1,-y1),
设直线PA的方程为y=k(x-3),
联立方程组
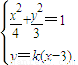 ,消掉y,化简整理得(4k2+3)x2-24k2x+36k2-12=0,
,消掉y,化简整理得(4k2+3)x2-24k2x+36k2-12=0,由△=(24k2)2-4•(3+4k2)•(36k2-12)>0,得
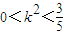 .
.则
 .
.直线BC的方程为:
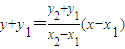 ,
,令y=0,则
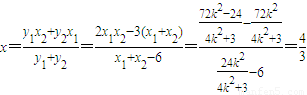 .
.∴Q点坐标为
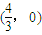 .
.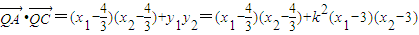
=

=

=
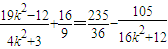 .
.∵
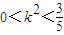 ,
,∴
 .
.点评:本题考查直线、椭圆方程及其位置关系,考查向量的数量积运算,考查函数思想,考查学生分析解决问题的能力,综合性强,难度较大,对能力要求较高.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案
相关题目
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+2相切,
,以原点为圆心,椭圆短半轴长半径的圆与直线y=x+2相切,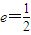 的椭圆
的椭圆 的左、右焦点分别为F1、F2,P是x轴正半轴上一点,以PF1为直径的圆经过椭圆M短轴端点,且该圆和直线
的左、右焦点分别为F1、F2,P是x轴正半轴上一点,以PF1为直径的圆经过椭圆M短轴端点,且该圆和直线 相切,过点P直线椭圆M相交于相异两点A、C.
相切,过点P直线椭圆M相交于相异两点A、C.