题目内容
设A(1,0,0),B(1,0,1),C(0,1,1)D(1,1,1),求直线AD与平面ABC所成的角.
分析:设平面ABC的法向量为
=(x,y,z),利用线面垂直即可得出.设直线AD与平面ABC所成的角为θ,利用sinθ=|cos<
,
>|=
即可求出.
| n |
| n |
| AD |
|
| ||||
|
|
解答:解:∵A(1,0,0),B(1,0,1),C(0,1,1),∴
=(0,0,1),
=(-1,1,1).
设平面ABC的法向量为
=(x,y,z),则
,即
,
不妨令x=1,则y=1,z=0,∴
=(1,1,0).
又
=(0,1,1),
设直线AD与平面ABC所成的角为θ,
则sinθ=|cos<
,
>|=
=
=
.
∵θ∈[0,
],∴θ=
.
因此直线AD与平面ABC所成的角为
.
| AB |
| AC |
设平面ABC的法向量为
| n |
|
|
不妨令x=1,则y=1,z=0,∴
| n |
又
| AD |
设直线AD与平面ABC所成的角为θ,
则sinθ=|cos<
| n |
| AD |
|
| ||||
|
|
| 1 | ||||
|
| 1 |
| 2 |
∵θ∈[0,
| π |
| 2 |
| π |
| 6 |
因此直线AD与平面ABC所成的角为
| π |
| 6 |
点评:熟练掌握线面垂直的性质、垂直与数量积的关系、公式sinθ=|cos<
,
>|=
求线面角是解题的关键.
| n |
| AD |
|
| ||||
|
|

练习册系列答案
相关题目
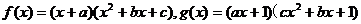 .记集合S=
.记集合S= 若
若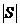 ,
,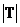 分别为集合元素S,T的元素个数,则下列结论不可能的是
分别为集合元素S,T的元素个数,则下列结论不可能的是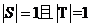
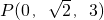 的距离等于到点Q(0,1,-1)的距离的两倍,那么A点的坐标是
的距离等于到点Q(0,1,-1)的距离的两倍,那么A点的坐标是 ,0,0)和(
,0,0)和( ,0,0)
,0,0) ,0,0)和(
,0,0)和( ,0,0)
,0,0)