题目内容
已知函数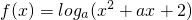
(1)若定义域为R,求a范围
(2)若值域为R,求a范围.
解:(1)由函数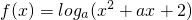 的定义域为R,
的定义域为R,
说明x2+ax+2>0对任意实数恒成立,
则不等式x2+ax+2>0对应二次方程的△=a2-8<0,即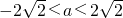 .
.
又a>0且a≠1,所以,0<a< ,且a≠1.
,且a≠1.
故使函数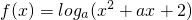 的定义域为R的a的取值范围是(0,1)∪(1,
的定义域为R的a的取值范围是(0,1)∪(1, );
);
(2)函数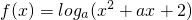 的值域为R,
的值域为R,
说明x2+ax+2能取到大于0的所有实数,
则不等式x2+ax+2>0对应二次方程的△=a2-8≥0,解得: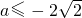 或
或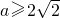 .
.
又a>0且a≠1,所以,使函数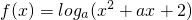 的值域为R的a的取值范围是(2
的值域为R的a的取值范围是(2 ,+∞).
,+∞).
分析:(1)根据函数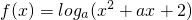 的定义域为R,说明对任意实数x,对数式的真数恒大于0,而真数是二次三项式,由其对应的二次方程的判别式小于0即可求得a的取值范围,同时兼顾对数式的底数有意义;
的定义域为R,说明对任意实数x,对数式的真数恒大于0,而真数是二次三项式,由其对应的二次方程的判别式小于0即可求得a的取值范围,同时兼顾对数式的底数有意义;
(2)根据函数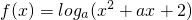 的值域为R,说明对数式的真数能取到大于0的所有实数,则真数上的二次三项式对应的抛物线顶点应在x轴上或其下方,故其对应的二次方程的判别式应大于等于0,由此求解a的取值范围.
的值域为R,说明对数式的真数能取到大于0的所有实数,则真数上的二次三项式对应的抛物线顶点应在x轴上或其下方,故其对应的二次方程的判别式应大于等于0,由此求解a的取值范围.
点评:本题考查了函数的定义域,函数的值域,考查了数学转化思想,解答此题的关键是由函数值域是R,得到真数的二次三项式的判别式大于等于0,是基础题,解答时易忽略底数的限制条件,也是易错题.
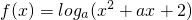 的定义域为R,
的定义域为R,说明x2+ax+2>0对任意实数恒成立,
则不等式x2+ax+2>0对应二次方程的△=a2-8<0,即
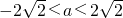 .
.又a>0且a≠1,所以,0<a<
 ,且a≠1.
,且a≠1.故使函数
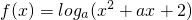 的定义域为R的a的取值范围是(0,1)∪(1,
的定义域为R的a的取值范围是(0,1)∪(1, );
);(2)函数
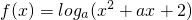 的值域为R,
的值域为R,说明x2+ax+2能取到大于0的所有实数,
则不等式x2+ax+2>0对应二次方程的△=a2-8≥0,解得:
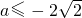 或
或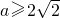 .
.又a>0且a≠1,所以,使函数
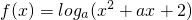 的值域为R的a的取值范围是(2
的值域为R的a的取值范围是(2 ,+∞).
,+∞).分析:(1)根据函数
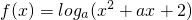 的定义域为R,说明对任意实数x,对数式的真数恒大于0,而真数是二次三项式,由其对应的二次方程的判别式小于0即可求得a的取值范围,同时兼顾对数式的底数有意义;
的定义域为R,说明对任意实数x,对数式的真数恒大于0,而真数是二次三项式,由其对应的二次方程的判别式小于0即可求得a的取值范围,同时兼顾对数式的底数有意义;(2)根据函数
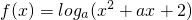 的值域为R,说明对数式的真数能取到大于0的所有实数,则真数上的二次三项式对应的抛物线顶点应在x轴上或其下方,故其对应的二次方程的判别式应大于等于0,由此求解a的取值范围.
的值域为R,说明对数式的真数能取到大于0的所有实数,则真数上的二次三项式对应的抛物线顶点应在x轴上或其下方,故其对应的二次方程的判别式应大于等于0,由此求解a的取值范围.点评:本题考查了函数的定义域,函数的值域,考查了数学转化思想,解答此题的关键是由函数值域是R,得到真数的二次三项式的判别式大于等于0,是基础题,解答时易忽略底数的限制条件,也是易错题.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
 .
. ,当
,当 时,求
时,求 的取值范围;
的取值范围; 上奇函数
上奇函数 满足
满足 ,且当
,且当 时,
时, ,求
,求 在
在 上的反函数
上的反函数 ;
; 的不等式
的不等式 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围.
的取值范围. .
. ,当
,当 时,求
时,求 的取值范围;
的取值范围; 上奇函数
上奇函数 满足
满足 ,且当
,且当 时,
时, ,求
,求 在
在 上的反函数
上的反函数 ;
;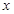 的不等式
的不等式 在
在 的取值范围.
的取值范围.
 在
在 上是增函数,
上是增函数,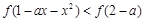 对于任意
对于任意 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。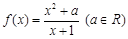 .
. 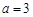 时,函数
时,函数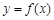 在
在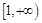 上是增函数;[来源:学.科.网Z.X.X.K]
上是增函数;[来源:学.科.网Z.X.X.K]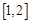 上有最小值
上有最小值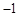 ,求实数
,求实数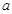 的值.
的值. =
=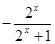 .
.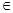 [1,2],求函数
[1,2],求函数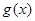 =
=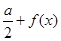 ,且当x
,且当x 恒成立,求实数
恒成立,求实数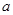 的取值范围.
的取值范围.