题目内容
已知函数 .
.
(1)若 ,当
,当 时,求
时,求 的取值范围;
的取值范围;
(2)若定义在 上奇函数
上奇函数 满足
满足 ,且当
,且当 时,
时, ,求
,求 在
在 上的反函数
上的反函数 ;
;
(3)若关于 的不等式
的不等式 在区间
在区间 上有解,求实数
上有解,求实数 的取值范围.
的取值范围.
【答案】
(1) ;(2);(3).
;(2);(3).
【解析】
试题分析:(1)这实质上是解不等式 ,即
,即 ,但是要注意对数的真数要为正,
,但是要注意对数的真数要为正, ,
, ;(2)
;(2) 上奇函数
上奇函数 满足
满足 ,可很快求出
,可很快求出 ,要求
,要求 在
在 上的反函数,必须求出
上的反函数,必须求出 在
在 上的解析式,当
上的解析式,当 时,
时, ,故
,故 ,当然求反函数还要求出反函数的定义域即原函数的值域;(3)
,当然求反函数还要求出反函数的定义域即原函数的值域;(3) 可转化为
可转化为 ,这样利用对数函数的性质得
,这样利用对数函数的性质得 ,变成了整式不等式,问题转化为不等式
,变成了整式不等式,问题转化为不等式 在区间
在区间 上有解,而这个问题通常采用分离参数法,转化为求相应函数的值域或最值.
上有解,而这个问题通常采用分离参数法,转化为求相应函数的值域或最值.
试题解析:(1)原不等式可化为 1分
1分
所以 ,
, ,
, 1分
1分
得 2分
2分
(2)因为 是奇函数,所以
是奇函数,所以 ,得
,得 1分
1分
当 时,
时,
 2分
2分
此时 ,
, ,所以
,所以
 2分
2分
(3)由题意 , 1分
, 1分
即 1分
1分
所以不等式 在区间
在区间 上有解,
上有解,
即 3分
3分
所以实数 的取值范围为
的取值范围为 1分
1分
考点:(1)对数不等式;(2)分段函数的反函数;(3)不等式有解问题.

练习册系列答案
 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
 ,
,
 ,求
,求 的单调区间;
的单调区间; 时,求证:
时,求证: .
.
 .
. 为
为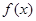 的极值点,求实数
的极值点,求实数 的值;
的值; 在
在 上为增函数,求实数
上为增函数,求实数 时,方程
时,方程 有实根,求实数
有实根,求实数 的最大值.
的最大值. 。
。 ,求函数
,求函数 的值;
的值; .
.
 中任取一个元素
中任取一个元素 ,从集合
,从集合 中任取一个元素
中任取一个元素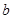 ,求方程
,求方程 有两个不相等实根的概率;
有两个不相等实根的概率; 中任取的一个数,
中任取的一个数, 中任取的一个数,求方程
中任取的一个数,求方程