题目内容
已知平面内有一条线段AB,其长为6,动点P满足PA-PB=4,O为AB的中点,则PO的最小值为________.
2
分析:建立适当坐标系,利用双曲线的定义可求得双曲线的标准方程,从而可得PO的最小值.
解答:以AB所在的直线为x轴,以AB的垂直平分线为y轴建立直角坐标系,则A(-3,0),B(3,0)
∵|AB|=6=2c,PA-PB=4=2a,O为AB的中点,
∴b2=c2-a2=5,
∴动点P的轨迹方程为: -
- =1(x≥2),
=1(x≥2),
∴PO的最小值为:2.
故答案为:2.
点评:本题考查双曲线的定义及标准方程,掌握双曲线的标准方程及性质是关键,属于基础题.
分析:建立适当坐标系,利用双曲线的定义可求得双曲线的标准方程,从而可得PO的最小值.
解答:以AB所在的直线为x轴,以AB的垂直平分线为y轴建立直角坐标系,则A(-3,0),B(3,0)
∵|AB|=6=2c,PA-PB=4=2a,O为AB的中点,
∴b2=c2-a2=5,
∴动点P的轨迹方程为:
 -
- =1(x≥2),
=1(x≥2),∴PO的最小值为:2.
故答案为:2.
点评:本题考查双曲线的定义及标准方程,掌握双曲线的标准方程及性质是关键,属于基础题.

练习册系列答案
相关题目
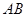 ,其长度为4,动点
,其长度为4,动点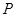 满足
满足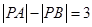 ,
,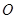 为
为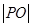 的最小值为( )
的最小值为( )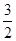 B.1 C.2 D.3
B.1 C.2 D.3