题目内容
(本小题满分10分)选修4-4:坐标系与参数方程
已知曲线 的参数方程为
的参数方程为 (
( 为参数),在同一平面直角坐标系中,将曲线
为参数),在同一平面直角坐标系中,将曲线 上的点按坐标变换
上的点按坐标变换 得到曲线
得到曲线 .(1)求曲线
.(1)求曲线 的普通方程; (2)若点
的普通方程; (2)若点 在曲线
在曲线 上,点
上,点
 ,当点
,当点 在曲线
在曲线 上运动时,求
上运动时,求 中点
中点 的轨迹方程.
的轨迹方程.
(1) ;(2)
;(2)
【解析】
试题分析:(1)将参数方程转化为直角坐标系下的普通方程,需要根据参数方程的结构特征,选取恰当的消参方法,常见的消参方法有:代入消参法、加减消参法、平方消参法;(2)将参数方程转化为普通方程时,要注意两种方程的等价性,不要增解、漏解,若 有范围限制,要标出
有范围限制,要标出 的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式
的取值范围;(3)直角坐标方程化为极坐标方程,只需把公式 及
及 直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如
直接代入并化简即可;而极坐标方程化为极坐标方程要通过变形,构造形如 ,
, ,
, 的形式,进行整体代换,其中方程的两边同乘以(或同除以)
的形式,进行整体代换,其中方程的两边同乘以(或同除以) 及方程的两边平方是常用的变形方法.
及方程的两边平方是常用的变形方法.
试题解析:(1) :
:

 ,
,
将

 代入
代入 的普通方程得
的普通方程得 ,即
,即 ;
;
(2)设

 , 则
, 则
所以 ,即
,即
代入 ,得
,得 ,即
,即
 中点
中点 的轨迹方程为
的轨迹方程为 .
.
考点:1、参数方程与普通方程的互化;2、点的轨迹方程.
考点分析: 考点1:参数方程 试题属性- 题型:
- 难度:
- 考核:
- 年级:

练习册系列答案
 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案
相关题目
 为虚数单位,则
为虚数单位,则 等于( )
等于( ) B.
B. C.
C. D.
D.
 与圆
与圆 的位置关系是( )
的位置关系是( )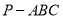 中,
中,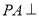 平面
平面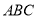 ,
, ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )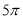 B.
B.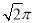 C.
C. D.
D.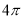
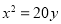 的焦点重合,且其渐近线的方程为
的焦点重合,且其渐近线的方程为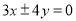 ,则该双曲线的标准方程为( )
,则该双曲线的标准方程为( )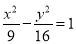 B.
B.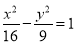 C.
C. D.
D.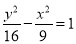
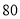 小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段
小时的社区服务才合格.教育部门在全市随机抽取200位学生参加社区服务的数据,按时间段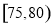 ,
,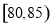 ,
,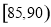 ,
,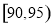 ,
,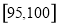 (单位:小时)进行统计,其频率分布直方图如图所示.
(单位:小时)进行统计,其频率分布直方图如图所示.
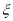 为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量
为3位学生中参加社区服务时间不少于90小时的人数.试求随机变量 .
.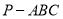 中,
中,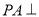 平面
平面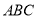 ,
,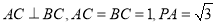 ,则该三棱锥外接球的表面积为( )
,则该三棱锥外接球的表面积为( )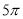 B.
B.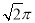 C.
C.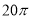 D.
D.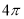
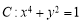 ,给出下列四个命题:
,给出下列四个命题: 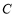 关于原点对称;
关于原点对称; 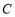 关于直线
关于直线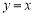 对称
对称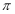
 、
、 、
、 、
、 的四个小球,从盒子里随机摸出两个小球,那么事件“摸出的小球上标有的数字之和为
的四个小球,从盒子里随机摸出两个小球,那么事件“摸出的小球上标有的数字之和为 ”的概率是 .
”的概率是 .