题目内容
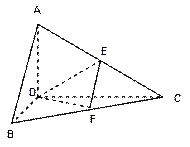
如图,四棱锥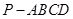 中,底面
中,底面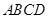 是平行四边形,
是平行四边形,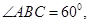
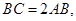
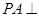 底面
底面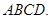
(Ⅰ)求证: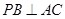 ;(Ⅱ)若
;(Ⅱ)若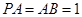 ,求二面角
,求二面角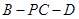 的余弦值;
的余弦值;
(Ⅲ)当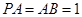 时,在线段
时,在线段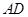 上是否存在一点
上是否存在一点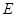 使二面角
使二面角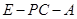 为
为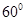 ,若存在,试确定点
,若存在,试确定点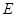 的位置;若不存在,请说明理由。
的位置;若不存在,请说明理由。

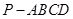 中,底面
中,底面 是平行四边形,
是平行四边形,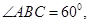
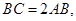
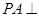 底面
底面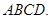
(Ⅰ)求证:
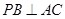 ;(Ⅱ)若
;(Ⅱ)若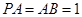 ,求二面角
,求二面角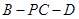 的余弦值;
的余弦值;(Ⅲ)当
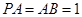 时,在线段
时,在线段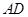 上是否存在一点
上是否存在一点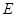 使二面角
使二面角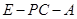 为
为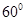 ,若存在,试确定点
,若存在,试确定点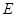 的位置;若不存在,请说明理由。
的位置;若不存在,请说明理由。
(Ⅰ)证明:在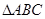 中,
中,
∵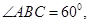
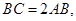
∴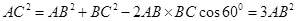
∴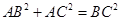 ,得
,得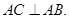
又∵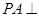 底面
底面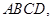
∴斜线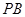 在底面
在底面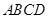 内的射影为
内的射影为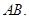
∴由三垂线定理,得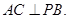
故,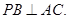 …………………………………4分
…………………………………4分
(Ⅱ)以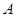 为原点,
为原点,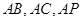 分别为
分别为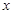 轴、
轴、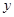 轴、
轴、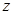 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则
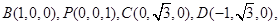
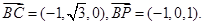
设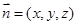 是平面
是平面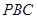 的法向量,则
的法向量,则
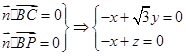 取
取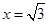 ,
,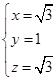 得
得
∴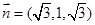 是平面
是平面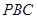 的一个法向量。
的一个法向量。
同理可求: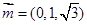 是平面
是平面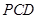 的一个法向量
的一个法向量
∴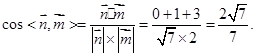 ………………………………7分
………………………………7分
故,二面角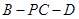 的余弦值
的余弦值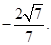
(Ⅲ)显然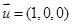 是平面
是平面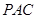 的一个法向量,可是
的一个法向量,可是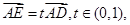
因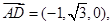 得
得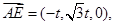 从而,得
从而,得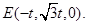
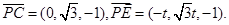
设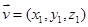 是平面
是平面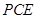 的法向量,同(Ⅱ)容易解得
的法向量,同(Ⅱ)容易解得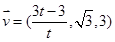 是平面
是平面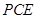 的一个法向量。
的一个法向量。
由题意,得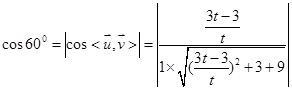 ………………12分
………………12分
即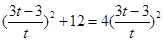 ,注意到
,注意到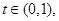 解得
解得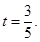
故,当点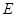 在线段
在线段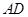 上,且满足
上,且满足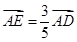 时,二面角
时,二面角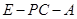 为
为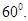
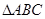 中,
中,∵
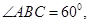
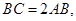
∴
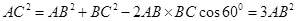
∴
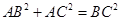 ,得
,得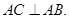
又∵
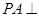 底面
底面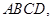
∴斜线
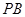 在底面
在底面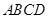 内的射影为
内的射影为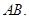
∴由三垂线定理,得
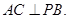
故,
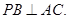 …………………………………4分
…………………………………4分(Ⅱ)以
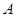 为原点,
为原点,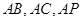 分别为
分别为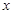 轴、
轴、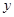 轴、
轴、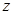 轴建立空间直角坐标系,则
轴建立空间直角坐标系,则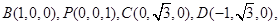
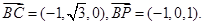
设
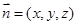 是平面
是平面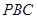 的法向量,则
的法向量,则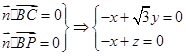 取
取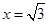 ,
,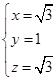 得
得∴
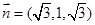 是平面
是平面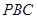 的一个法向量。
的一个法向量。同理可求:
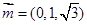 是平面
是平面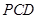 的一个法向量
的一个法向量∴
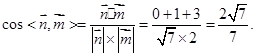 ………………………………7分
………………………………7分故,二面角
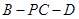 的余弦值
的余弦值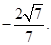
(Ⅲ)显然
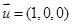 是平面
是平面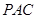 的一个法向量,可是
的一个法向量,可是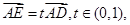
因
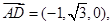 得
得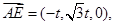 从而,得
从而,得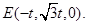
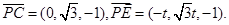
设
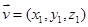 是平面
是平面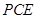 的法向量,同(Ⅱ)容易解得
的法向量,同(Ⅱ)容易解得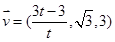 是平面
是平面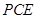 的一个法向量。
的一个法向量。由题意,得
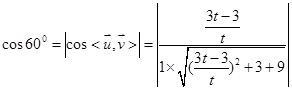 ………………12分
………………12分即
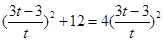 ,注意到
,注意到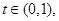 解得
解得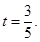
故,当点
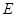 在线段
在线段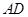 上,且满足
上,且满足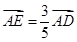 时,二面角
时,二面角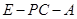 为
为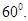
略

练习册系列答案
相关题目

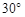
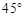
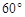
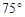
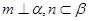 .下面有四个命题( )
.下面有四个命题( )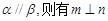 ; (2)
; (2)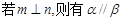 ;
;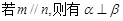 ; (4)
; (4)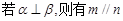 .
.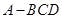 中,侧棱
中,侧棱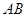 、
、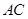 、
、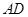 两两垂直,
两两垂直,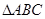 、
、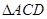 、
、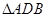 的面积分别为
的面积分别为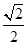 、
、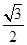 、
、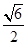 ,则该三棱锥外接球的表面积为
,则该三棱锥外接球的表面积为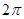
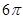
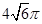
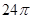
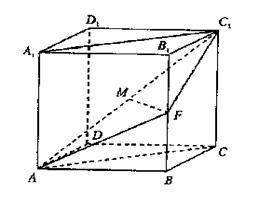
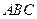 的边长为4,
的边长为4,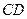 是
是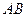 边上的高,
边上的高,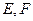 分别是
分别是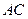 和
和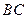 边的中点,现将△
边的中点,现将△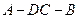 .
.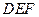 的位置关系,并说明理由;
的位置关系,并说明理由;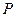 ,使
,使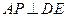 ?证明你的结论.
?证明你的结论.
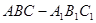 的体积为
的体积为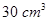 ,
,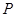 为其侧棱
为其侧棱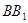 上的任意一点,则四棱锥
上的任意一点,则四棱锥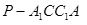 的体积为____________
的体积为____________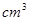 .
.