题目内容
设函数f(x)的解析式满足f(x+1)=
(a>0).
(1)求函数f(x)的解析式;
(2)当a=1时,试判断函数f(x)在区间(0,+∞)上的单调性,并加以证明;
(3)当a=1时,记函数g(x)=
,求函数g(x)在区间[-2,-
]上的值域.
| x2+2x+a+1 |
| x+1 |
(1)求函数f(x)的解析式;
(2)当a=1时,试判断函数f(x)在区间(0,+∞)上的单调性,并加以证明;
(3)当a=1时,记函数g(x)=
|
| 1 |
| 2 |
(1)设x+1=t(t≠0),则x=t-1,
∴f(t)=
=
∴f(x)=
(2)当a=1时,f(x)=
=x+
f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
证明:设0<x1<x2<1,则f(x1)-f(x2)=(x1+
)-(x2+
)=(x1-x2)+(
-
)=(x1-x2)+
(x1-x2)(1-
)=
(x1x2-1)(8分)
∵0<x1<x2<1,∴x1-x2<0,x1x2>0,x1x2-1<0,
∴
(x1x2-1)>0,∴f(x1)-f(x2)>0?f(x1)>f(x2)
所以,f(x)在(0,1)上单调递减,
同理可证得f(x)在(1,+∞)上单调递增
(3)∵g(-x)=
=
=g(x),
∴g(x)为偶函数,
所以,∴y=g(x)的图象关于y轴对称,
又当a=1,x∈[
,2]时,由(2)知g(x)=x+
在[
,1]单调减,[1,2]单调增,
∴g(x)min=g(1)=2,g(x)max=g(
)=g(2)=
∴当a=1时,函数g(x)在区间[-2,-
]上的值域的为[2,
]
∴f(t)=
| (t-1)2+2(t-1)+2a+1 |
| t |
| t2+a |
| t |
∴f(x)=
| x2+a |
| x |
(2)当a=1时,f(x)=
| x2+1 |
| x |
| 1 |
| x |
f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,
证明:设0<x1<x2<1,则f(x1)-f(x2)=(x1+
| 1 |
| x1 |
| 1 |
| x2 |
| 1 |
| x1 |
| 1 |
| x2 |
| x2-x1 |
| x1x2 |
| 1 |
| x1x2 |
| (x1-x2) |
| x1x2 |
∵0<x1<x2<1,∴x1-x2<0,x1x2>0,x1x2-1<0,
∴
| (x1-x2) |
| x1x2 |
所以,f(x)在(0,1)上单调递减,
同理可证得f(x)在(1,+∞)上单调递增
(3)∵g(-x)=
|
|
∴g(x)为偶函数,
所以,∴y=g(x)的图象关于y轴对称,
又当a=1,x∈[
| 1 |
| 2 |
| 1 |
| x |
| 1 |
| 2 |
∴g(x)min=g(1)=2,g(x)max=g(
| 1 |
| 2 |
| 5 |
| 2 |
∴当a=1时,函数g(x)在区间[-2,-
| 1 |
| 2 |
| 5 |
| 2 |

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
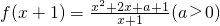 .
.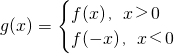 ,求函数g(x)在区间
,求函数g(x)在区间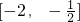 上的值域.
上的值域.