题目内容
已知tanα=2,求
解法一:∵sin2α+cos2α=1,
∴(cosαtanα)2+cos2α=1.∴cos2α=![]() .
.
又∵tanα=2,
∴cos2α=![]() ,
,
sin2α=tan2αcos2α=![]() .
.
∴原式=![]() sin2α-tanαcos2α+
sin2α-tanαcos2α+![]() cos2α=
cos2α=![]() ×
×![]() -2×
-2×![]() +
+![]() ×
×![]() =
=![]() .
.
解法二:∵tanα=2,∴α的终边不落在坐标轴上.
∴cosα≠0.
原式=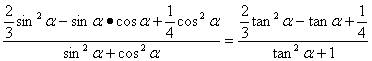
=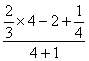 =
=![]() .
.

练习册系列答案
 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案
相关题目
 =2,求
=2,求 =
.
=
. 的值. (2)求
的值. (2)求 的值.
的值. = 2 ,求
= 2 ,求 的值
.
的值
.