题目内容
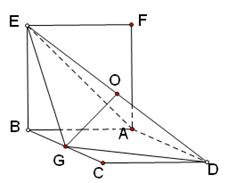 如图,正方形
如图,正方形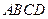 和
和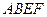 的边长均为1,且它们所在平面互相垂直,
的边长均为1,且它们所在平面互相垂直,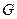 为线段
为线段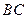 的中点,
的中点, 为线段
为线段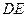 的中点。
的中点。(1)求证:
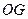 ∥面
∥面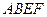 ;
;(2)求证:平面
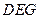 ⊥平面
⊥平面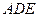 ;
;(3)求直线
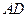 与平面
与平面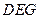 所成角的正切值.
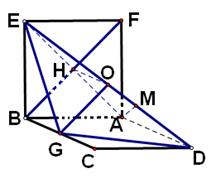
所成角的正切值. (1) (2)证明如下 (3)tan∠ADE=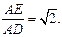
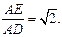
 (1)证:连结BF,与AE交于点H,连结OH,
(1)证:连结BF,与AE交于点H,连结OH, ∵点O、H分别是线段DE、AE的中点,
∴OH∥AD,且OH=
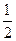 AD
AD 又∵BG∥AD,且BG=
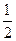 AD ,∴BG∥OH,且BG="OH"
AD ,∴BG∥OH,且BG="OH"  ∴四边形OHBG是平行四边形 ∴OG∥BH
∴四边形OHBG是平行四边形 ∴OG∥BH 
又 ∵BH
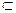 平面ABEF,OG
平面ABEF,OG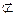 平面ABEF,
平面ABEF,∴OG∥面ABEF
(2)证明:∵正方形ABCD和ABEF所在平面互相垂直,AD⊥AB,AB=平面ABCD∩平面ABEF,
∴AD⊥平面ABEF, 又BF
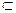 平面ABEF,∴AD⊥BF
平面ABEF,∴AD⊥BF在正方形ABEF中,BF⊥AE,AD∩AE=A,∴BF⊥平面ADE,
由(1)知OG∥BF,∴OG⊥平面ADE, 又OG
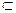 平面DEG,
平面DEG,∴平面DEG⊥平面ADE
(3)作AM⊥DE,垂足为点M,DE=平面DEG∩平面ADE
由(2)已证得平面DEG⊥平面ADE, 则AM⊥平面DEG,
∴∠ADM即∠ADE为直线AD与平面DEG所成的角
∴在Rt△ADE中,tan∠ADE=
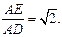

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目
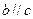 ,且直线
,且直线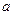 与
与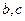 都相交,求证:直线
都相交,求证:直线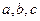 共面。
共面。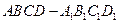 中,
中,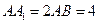 ,点
,点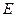 在
在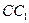 上
上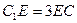 .
.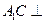 平面
平面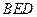 ;(2)求二面角
;(2)求二面角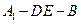 的大小.
的大小.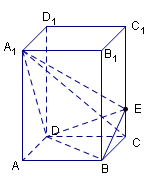
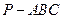 高为2,侧棱与底面所成角为
高为2,侧棱与底面所成角为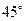 ,则点
,则点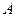 到侧面
到侧面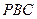 的距离是
的距离是 ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
ACB = 120°,DABC所在平面外的一点P到三角形三顶点的距离都等于4,求直线PC与平面ABC所成的角。
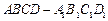 中,已知底面
中,已知底面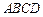 是边长为4的菱形,
是边长为4的菱形,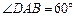 ,且点
,且点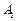 在面
在面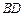 与AC的交点O,设点E是
与AC的交点O,设点E是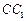 的中点,
的中点,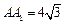 .
.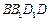 是矩形;
是矩形;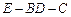 的大小;
的大小;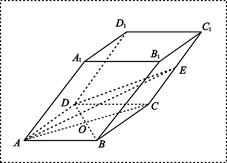 (Ⅲ) 求四面体
(Ⅲ) 求四面体 的体积.
的体积. 的平面去截球,所得的截面面积为
的平面去截球,所得的截面面积为 ,则球的体积为( )
,则球的体积为( )



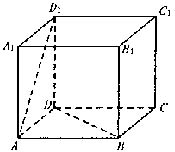 如图,正方体ABCD—A1B1C1D1的棱长为1,PQ分别是线段AD1和BD上的点,且D1P∶PA=DQ∶QB=5∶12.
如图,正方体ABCD—A1B1C1D1的棱长为1,PQ分别是线段AD1和BD上的点,且D1P∶PA=DQ∶QB=5∶12. 为正三角形,AB
为正三角形,AB 平面PBC,AB//CD,AB=
平面PBC,AB//CD,AB= DC,E为PD中点。(1)求证:AE//平面PBC
DC,E为PD中点。(1)求证:AE//平面PBC