题目内容
已知过椭圆| x2 |
| a2 |
| y2 |
| b2 |
| AF |
| FB |
分析:设出A、B两点的坐标,A(m,m-c),B( n,n-c),由
=2
得 m+2n=3c ①,再根据椭圆的第二定义,
=2=
,可得 2n-m=
②,由①②解得 m 和 n的值,再代入椭圆的第二定义,e=
=
=
,解方程求得e的值.
| AF |
| FB |
| AF |
| FB |
| ||
|
| a2 |
| c |
| BF |
| d |
| ||
|
| ||||
| 3-3e2 |
解答:解:右焦点F(c,0),直线的方程为 y-0=x-c. 设 A(m,m-c),B( n,n-c),
由
=2
得 (c-m,c-m)=2 (n-c,n-c),∴c-m=2(n-c),m+2n=3c ①.
再根据椭圆的第二定义,
=2=
,∴2n-m=
②,
由①②解得 m=
,n=
.
据椭圆的第二定义,e=
=
=
=
=
,
∴3e3-3e-
e2+
=0,(e2-1)•(3e-
)=0.∵0<e<1,
∴e=
,故椭圆的离心率是
,故答案为
.
由
| AF |
| FB |
再根据椭圆的第二定义,
| AF |
| FB |
| ||
|
| a2 |
| c |
由①②解得 m=
| 3c2-a2 |
| 2c |
| 3c2+a2 |
| 4c |
据椭圆的第二定义,e=
| BF |
| d |
| ||
|
| ||||
|
=
| ||||
| 3a2-3c2 |
| ||||
| 3-3e2 |
∴3e3-3e-
| 2 |
| 2 |
| 2 |
∴e=
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
点评:本题考查椭圆的定义、椭圆的标准方程,以及椭圆的简单性质的应用.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
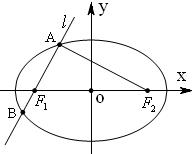 如图已知,椭圆
如图已知,椭圆 如图,已知:椭圆
如图,已知:椭圆 如图,已知过椭圆
如图,已知过椭圆