题目内容
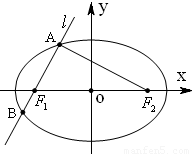
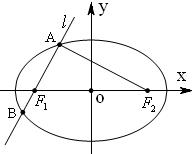 如图已知,椭圆
如图已知,椭圆| x2 |
| a2 |
| y2 |
| b2 |
(Ⅰ)若∠AF1F2=60°,且
| AF1 |
| AF2 |
(Ⅱ)若a=
| 2 |
| F1A |
| F1B |
分析:(Ⅰ)因为在焦点三角形AF1F2中,
•
=0,所以∠F1AF2=90°,又因为∠AF1F2=60°,所以△AF1F2的三边关系可以找到,根据三边关系,可求出含a,c的齐次式,进而求出离心率.
(II)若a=
,b=1,则椭圆方程为两个,可以是焦点在x轴上,也可焦点在y轴上,分别写出方程,在与设出的直线l方程联立,找到横坐标之和与之积,用坐标表示
•
,根据前面所求,得到含k的方程,再求出最值即可.
| AF1 |
| AF2 |
(II)若a=
| 2 |
| F1A |
| F1B |
解答:解:(I)∵
•
=0,∴AF1⊥AF2∵∠AF1F2=60°,∴F1F2=2AF1,AF2=
AF1------(3分)
∴2a=AF1+AF2,2c=F1F2∴离心率e=
=
=
-1------(6分)
(II)∵a=
,b=1,∴c=1,点F1(-1,0),F2(1,0).
①若AB垂直于x轴,则A(-1,
),B(-1,-
),
•
=(0,
)•(0,-
)=-
------(8分)
②若AB与x轴不垂直,设直线AB的斜率为k,
则直线AB的方程为 y=k(x+1)
由
消去y得:(2k2+1)x2+4k2x+2k2-2=0∵△=8k2+8>0,∴方程有两个不等的实数根.
设A(x1,y1),B(x2,y2).∴x1+x2=-
,x1•x2=
------(10分)
∴
=(x1+1,y1),
=(x2+1,y2)
•
=(x1+1)(x2+1)+y1y2=(x1+1)(x2+1)+k2(x1+1)(x2+1)=(1+k2)(x1x2+x1+x2+1)=(1+k2)(
-
+1)=-
=-
-
-------(12分)
∵k2≥0,2k2+1≥1, 0<
≤1,∴-1≤-
-
<-
∴
•
∈[-1,-
)------(14分)
综合①、②可得:
•
∈[-1,-
].
所以当直线l垂直于x时,
•
取得最大值-
;当直线l与x轴重合时,
•
取得最小值-1------(15分)
| AF1 |
| AF2 |
| 3 |
∴2a=AF1+AF2,2c=F1F2∴离心率e=
| c |
| a |
| F1F2 |
| AF1+AF2 |
| 3 |
(II)∵a=
| 2 |
①若AB垂直于x轴,则A(-1,
| ||
| 2 |
| ||
| 2 |
| F1A |
| F1B |
| ||
| 2 |
| ||
| 2 |
| 1 |
| 2 |
②若AB与x轴不垂直,设直线AB的斜率为k,
则直线AB的方程为 y=k(x+1)
由
|
设A(x1,y1),B(x2,y2).∴x1+x2=-
| 4k2 |
| 2k2+1 |
| 2k2-2 |
| 2k2+1 |
∴
| F1A |
| F1B |
| F1A |
| F1B |
| 2k2-2 |
| 2k2+1 |
| 4k2 |
| 2k2+1 |
| k2+1 |
| 2k2+1 |
| 1 |
| 2 |
| 1 |
| 2(2k2+1) |
∵k2≥0,2k2+1≥1, 0<
| 1 |
| 2k2+1 |
| 1 |
| 2 |
| 1 |
| 2(2k2+1) |
| 1 |
| 2 |
∴
| F1A |
| F1B |
| 1 |
| 2 |
综合①、②可得:
| F1A |
| F1B |
| 1 |
| 2 |
所以当直线l垂直于x时,
| F1A |
| F1B |
| 1 |
| 2 |
| F1A |
| F1B |
点评:本题考查了利用焦点三角形三边关系求椭圆方程,以及椭圆与向量相结合求最值,注意解题过程中,设而不求思想的应用.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
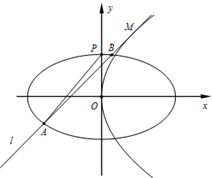 如图,已知:椭圆
如图,已知:椭圆 的左、右焦点分别为
的左、右焦点分别为 、
、 ,过
,过 与椭圆相交于A、B两点。
与椭圆相交于A、B两点。 ,且
,且 ,求椭圆的离心率;
,求椭圆的离心率; 求
求 的最大值和最小值。
的最大值和最小值。
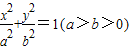 的左、右焦点分别为F1、F2,过F1的直线l与椭圆相交于A、B两点.
的左、右焦点分别为F1、F2,过F1的直线l与椭圆相交于A、B两点.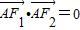 ,求椭圆的离心率;
,求椭圆的离心率;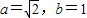 ,求
,求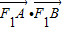 的最大值和最小值.
的最大值和最小值.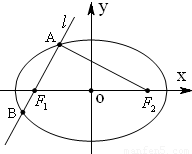
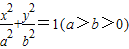 的左、右焦点分别为F1、F2,过F1的直线l与椭圆相交于A、B两点.
的左、右焦点分别为F1、F2,过F1的直线l与椭圆相交于A、B两点.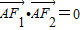 ,求椭圆的离心率;
,求椭圆的离心率;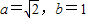 ,求
,求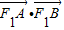 的最大值和最小值.
的最大值和最小值.