Question

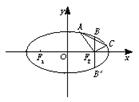
如图，已知：椭圆

x2

a2

+

y2

b2

=1（a＞b＞0）的上顶点为P，离心率e=

6

3

，长轴长为4

3

；点M为抛物线y²=6x上一动点，过M作抛物线的切线l与椭圆相交于不同的两点A，B．
（Ⅰ）试求椭圆的方程；
（Ⅱ）若∠APB为钝角，试求直线AB的斜率范围．

Answer 1

分析：（Ⅰ）利用椭圆的离心率e=

6

3

，长轴长为4

3

，求出几何量，即可求得椭圆的方程；
（Ⅱ）分类讨论，设出直线方程，分别代入椭圆、抛物线方程，利用韦达定理，及∠APB为钝角，即可求直线AB的斜率范围．

解答：解：（Ⅰ）由题意，椭圆的离心率e=

6

3

，长轴长为4

3

，
∴a=2

3

，c=2

2

∴b=

a2-c2

=2
∴椭圆的方程为

x2

12

+

y2

4

=1…（5分）
（Ⅱ）若直线斜率不存在，显然不合题意；
若斜率存在，则可设直线l：y=kx+t代入

x2

12

+

y2

4

=1化简得：（3k²+1）x²+6ktx+3t²-12=0
设A（x₁，y₁），B（x₂，y₂），则x1+x2=-

6kt

3k2+1

，x1x2=

3t2-12

3k2+1

，
∴y₁+y₂=k（x₁+x₂）+2t，y1y2=k2x1x2+kt(x1+x2)+t2…（8分）
△=36k²t²-4（3k²+1）（3t²-12）＞0得：12k²-t²+4＞0…（1）…（9分）
y=kx+t代入y²=6x得：k²x²+（2kt-6）x+t²=0
△=4k²t²-24kt+36-4k²t²=0，∴t=

3

2k

…（2）…（10分）
∵∠APB为钝角，∴

PA

•

PB

＜0
∴(x1，y1-2)•(x2，y2-2)=x1x2+k2x1x2+(kt-2k)(x1+x2)+t2-4t+4＜0
化简得：t²-t-2＜0解得：-1＜t＜2…（3）…（13分）
由（1）（2）得k2＞

31 -2

12

，∴k＜-

31 -2 12

或k＞

31 -2 12

由（2）（3）得  k=

3

2t

（-1＜t＜2）得：k＜-

3

2

或k＞

3

4

∴k＜-

3

2

或k＞

3

4

…（15分）

点评：本题考查椭圆的标准方程，考查直线与椭圆、抛物线的位置关系，考查韦达定理的运用，考查学生分析解决问题的能力，属于中档题．