Question

【题目】设函数，其中，，且．

（1）当时，函数在处的切线与直线平行，试求m的值；

（2）当时，令，若函数有两个极值点，且，求 的取值范围；

（3）当时，试讨论函数的零点个数，并证明你的结论．

Answer 1

【答案】（1）1；（2）；（3）见解析

【解析】

（1）求出导数，利用其意义就是斜率可求；

（2）求出的表达式，利用导数求出极值，可得范围；

（3）利用导数判断其单调性，结合零点存在定理可求.

（1）依题意得，，

∴

由题意知，

∴m=1

（2）由题意知：

则

令，得

故方程有两个不相等的正数根，（）

则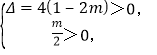解得

由方程得，且

由，得

，

，即函数是上的增函数，

所以，故的取值范围是

（3）依题意得，，

∴

令，得，∴，∵

∴函数在上单调递减，在上单调递增

∴

令（），则

∴

∴，即

∵，∴

又∵

∴

根据零点存在性定理知函数在和各有一个零点