Question

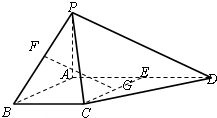（2013•浙江模拟）四棱锥P-ABCD中，PA⊥平面ABCD，E为AD的中点，ABCE为菱形，∠BAD=120°，PA=AB，G、F分别是线段CE、PB的中点．
（Ⅰ） 求证：FG∥平面PDC；
（Ⅱ） 求二面角F-CD-G的正切值．

Answer 1

分析：（I）连接BD与CE交于点G^′，利用平行线分线段成比例定理可证明G^′与点G重合．同理证明FG∥PD，利用线面平行的判定定理即可证明结论；
（II）通过建立空间直角坐标系，利用两个平面的法向量即可得出二面角的平面角．

解答：证明：（I）连接BD与CE交于点G^′，∵E为AD的中点，ABCE为菱形，
∴

CG′

G′E

=

BC

ED

=1，得到G^′为线段CE的中点，故G^′与点G重合．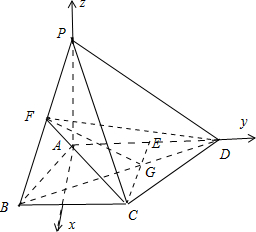
∵

BG

GD

=

BC

ED

=

BF

FP

=1，∴FG∥PD，
又∵FG?平面PDC，PD?平面PDC．
∴FG∥平面PDC．
（II）不妨设AB=2，则P （0，0，2），B(

3

，-1，0)，F(

3

2

，-

1

2

，1)，C(

3

，1，0)，D（0，4，0）．
∴

CD

=(-

3

，3，0)，

DF

=(

3

2

，-

9

2

，1)．
设平面CDF的法向量为

n

=(x，y，z)，则

n • CD =- 3 x+3y=0 n • DF = 3 2 x- 9 2 y+z=0

，令x=

3

，则y=1，z=3，
∴

n

=(

3

，1，3)．
取

m

=(0，0，1)作为平面GCD的法向量，
则cos＜

n

，

m

＞=

n • m

| n | | m |

=

3

13

，即为二面角的余弦值．
设二面角的平面角为θ，则cosθ=

3

13

，sinθ=

1-cos2θ

=

2

13

，∴tanθ=

sinθ

cosθ

=

2

3

．
∴二面角F-CD-G的正切值为

2

3

．

点评：熟练掌握平行线分线段成比例定理、菱形的性质、线面平行的判定定理、通过建立空间直角坐标系利用两个平面的法向量得出二面角的平面角的方法是解题的关键．