题目内容
函数f(x)=2x-sinx在x∈[0,2π]上的最大值为 .
考点:利用导数求闭区间上函数的最值
专题:计算题,导数的概念及应用
分析:求导数f'(x),由f'(x)的符号可判断f(x)的单调性,根据单调性可得f(x)的最大值.
解答:
解:f'(x)=2-cosx,
当x∈[0,2π]时,f'(x)>0,
∴f(x)在[0,2π]上单调递增,
故f(x)max=f(2π)=2×2π-sin2π=4π,
故答案为:4π.
当x∈[0,2π]时,f'(x)>0,
∴f(x)在[0,2π]上单调递增,
故f(x)max=f(2π)=2×2π-sin2π=4π,
故答案为:4π.
点评:本题考查利用导数求函数在闭区间上的最值问题,属中档题,正确理解导数与函数最值的关系是解题基础.

练习册系列答案
相关题目
对?a、b∈R,运算“⊕”、“?”定义为:a⊕b=
,a?b=
,则下列各式其中不恒成立的是( )
(1)a?b+a⊕b=a+b
(2)a?b-a⊕b=a-b
(3)[a?b]•[a⊕b]=a•b
(4)[a?b]÷[a⊕b]=a÷b.
|
|
(1)a?b+a⊕b=a+b
(2)a?b-a⊕b=a-b
(3)[a?b]•[a⊕b]=a•b
(4)[a?b]÷[a⊕b]=a÷b.
| A、(1)(3) |
| B、(2)(4) |
| C、(1)(2)(3) |
| D、(1)(2)(3)(4) |
已知等差数列{an}的前3项分别为4、6、8,则数列{an}的第4项为( )
| A、7 | B、8 | C、10 | D、12 |
已知等差数列{an}的前n项和为Sn,a5=5,S5=15,则数列{
}的前99和为( )
| 1 |
| anan+1 |
A、
| ||
B、
| ||
C、
| ||
D、
|
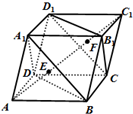 已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下命题,其中真命题有
已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.给出以下命题,其中真命题有