题目内容
已知椭圆 ,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心I,且有
,F1,F2为其左、右焦点,P为椭圆C上任一点,△F1PF2的重心为G,内心I,且有 (其中λ为实数),椭圆C的离心率e=
(其中λ为实数),椭圆C的离心率e=
- A.

- B.

- C.

- D.

A
分析:在焦点△F1PF2中,设P(x0,y0),由三角形重心坐标公式,可得重心G的纵坐标,因为 ,故内心I的纵坐标与G相同,最后利用三角形F1PF2的面积等于被内心分割的三个小三角形的面积之和建立a、b、c的等式,即可解得离心率
,故内心I的纵坐标与G相同,最后利用三角形F1PF2的面积等于被内心分割的三个小三角形的面积之和建立a、b、c的等式,即可解得离心率
解答:设P(x0,y0),∵G为△F1PF2的重心,
∴G点坐标为 G( ,
,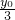 ),
),
∵ ,∴IG∥x轴,
,∴IG∥x轴,
∴I的纵坐标为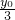 ,
,
在焦点△F1PF2中,|PF1|+|PF2|=2a,|F1F2|=2c
∴ =
= •|F1F2|•|y0|
•|F1F2|•|y0|
又∵I为△F1PF2的内心,∴I的纵坐标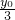 即为内切圆半径,
即为内切圆半径,
内心I把△F1PF2分为三个底分别为△F1PF2的三边,高为内切圆半径的小三角形
∴ =
= (|PF1|+|F1F2|+|PF2|)|
(|PF1|+|F1F2|+|PF2|)|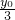 |
|
∴ •|F1F2|•|y0|=
•|F1F2|•|y0|= (|PF1|+|F1F2|+|PF2|)|
(|PF1|+|F1F2|+|PF2|)|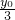 |
|
即 ×2c•|y0|=
×2c•|y0|= (2a+2c)|
(2a+2c)|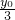 |,
|,
∴2c=a,
∴椭圆C的离心率e= =
=
故选A
点评:本题考查了椭圆的标准方程和几何意义,重心坐标公式,三角形内心的意义及其应用,椭圆离心率的求法
分析:在焦点△F1PF2中,设P(x0,y0),由三角形重心坐标公式,可得重心G的纵坐标,因为
 ,故内心I的纵坐标与G相同,最后利用三角形F1PF2的面积等于被内心分割的三个小三角形的面积之和建立a、b、c的等式,即可解得离心率
,故内心I的纵坐标与G相同,最后利用三角形F1PF2的面积等于被内心分割的三个小三角形的面积之和建立a、b、c的等式,即可解得离心率解答:设P(x0,y0),∵G为△F1PF2的重心,
∴G点坐标为 G(
 ,
,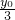 ),
),∵
 ,∴IG∥x轴,
,∴IG∥x轴,∴I的纵坐标为
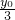 ,
,在焦点△F1PF2中,|PF1|+|PF2|=2a,|F1F2|=2c
∴
 =
= •|F1F2|•|y0|
•|F1F2|•|y0|又∵I为△F1PF2的内心,∴I的纵坐标
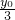 即为内切圆半径,
即为内切圆半径,内心I把△F1PF2分为三个底分别为△F1PF2的三边,高为内切圆半径的小三角形
∴
 =
= (|PF1|+|F1F2|+|PF2|)|
(|PF1|+|F1F2|+|PF2|)|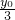 |
|∴
 •|F1F2|•|y0|=
•|F1F2|•|y0|= (|PF1|+|F1F2|+|PF2|)|
(|PF1|+|F1F2|+|PF2|)|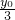 |
|即
 ×2c•|y0|=
×2c•|y0|= (2a+2c)|
(2a+2c)|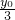 |,
|,∴2c=a,
∴椭圆C的离心率e=
 =
=
故选A
点评:本题考查了椭圆的标准方程和几何意义,重心坐标公式,三角形内心的意义及其应用,椭圆离心率的求法

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
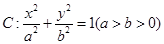 ,F1,F2为其左、右焦点,P为椭圆C上任一点,
,F1,F2为其左、右焦点,P为椭圆C上任一点,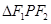 的重心为G,内心I,且有
的重心为G,内心I,且有 (其中
(其中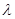 为实数),椭圆C的离心率e=( )
为实数),椭圆C的离心率e=( )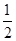 B.
B.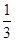 C.
C.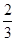 D.
D.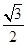
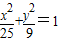 ,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )
,F1,F2分别为其左右焦点,椭圆上一点M到F1的距离是2,N是MF1的中点,则|ON|的长是( )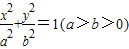 ,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .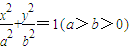 ,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .
,F1,F2是左右焦点,l是右准线,若椭圆上存在点P,使|PF1|是P到直线l的距离的2倍,则椭圆离心率的取值范围是 .