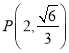题目内容
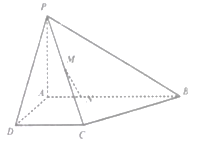
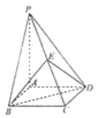
【题目】已知四棱柱![]() 的底面是边长为
的底面是边长为![]() 的菱形,且
的菱形,且![]() ,
,![]() 平面
平面![]() ,
,![]() ,设
,设![]() 为
为![]() 的中点
的中点
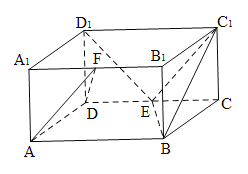
(1)求证:![]() 平面
平面![]()
(2)点![]() 在线段
在线段![]() 上,且
上,且![]() 平面
平面![]() ,求平面
,求平面![]() 和平面
和平面![]() 所成锐角的余弦值.
所成锐角的余弦值.
【答案】(1)证明略;(2)![]()
【解析】试题分析:(1)由已知该四棱柱为直四棱柱,且![]() 为等边三角形,
为等边三角形,![]() ,所以
,所以![]() 平面
平面![]() ,故
,故![]() ,在
,在![]() 中的三边长分别为
中的三边长分别为![]() ,所以
,所以![]() ,所以
,所以![]() ,故
,故![]() 平面
平面![]() ;
;
(2)取![]() 中点
中点![]() ,则由
,则由![]() 为等边三角形,知
为等边三角形,知![]() ,从而
,从而![]() ,以
,以![]() 为坐标轴,建立空间直角的坐标系,求得平面
为坐标轴,建立空间直角的坐标系,求得平面![]() 和平面
和平面![]() 的法向量,即可求得平面
的法向量,即可求得平面![]() 和平面
和平面![]() 所成锐角的余弦值.
所成锐角的余弦值.
试题解析:(1)证明:由已知该四棱柱为直四棱柱,且![]() 为等边三角形,
为等边三角形,![]()
所以![]() 平面
平面![]() ,而
,而![]() 平面
平面![]() ,故
,故![]()
因为![]() 的三边长分别为
的三边长分别为![]() ,故
,故![]() 为等腰直角三角形
为等腰直角三角形
所以![]() ,结合
,结合![]() 知:
知:![]() 平面
平面![]()
(2)解:取![]() 中点
中点![]() ,则由
,则由![]() 为等边三角形
为等边三角形

知![]() ,从而
,从而![]()
以![]() 为坐标轴,建立如图所示的坐标系
为坐标轴,建立如图所示的坐标系
此时![]() ,
,
![]() ,设
,设![]()
由上面的讨论知平面![]() 的法向量为
的法向量为![]()
由于![]() 平面
平面![]() ,故
,故![]() 平面
平面![]()
![]()
故![]() ,故
,故![]()
设平面![]() 的法向量为
的法向量为![]() ,
,![]()
由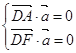 知
知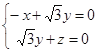 ,取
,取![]() ,故
,故![]()
设平面![]() 和平面
和平面![]() 所成锐角为
所成锐角为![]() ,则
,则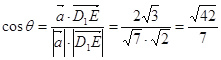
即平面![]() 和平面
和平面![]() 所成锐角的余弦值为
所成锐角的余弦值为![]()

 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
(1)已知产量![]() 和能耗
和能耗![]() 呈线性关系,请根据上表提供的数据,用最小二乘法求出
呈线性关系,请根据上表提供的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ;
;
(2)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?
参考公式: 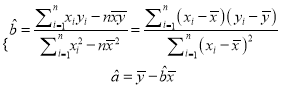
【题目】国家实行二孩生育政策后,为研究家庭经济状况对生二胎的影响,某机构在本地区符合二孩生育政策的家庭中,随机抽样进行了调查,得到如下的列联表:
经济状况好 | 经济状况一般 | 合计 | |
愿意生二胎 | 50 | ||
不愿意生二胎 | 20 | 110 | |
合计 | 210 |
(1)请完成上面的列联表,并判断能否在犯错误的概率不超过![]() 的前提下认为家庭经济状况与生育二胎有关?
的前提下认为家庭经济状况与生育二胎有关?
(2)若采用分层抽样的方法从愿意生二胎的家庭中随机抽取4个家庭,则经济状况好和经济状况一般的家庭分别应抽取多少个?
(3)在(2)的条件下,从中随机抽取2个家庭,求2个家庭都是经济状况好的概率.
附:![]()
|
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |