题目内容
已知向量
共线，则k=________．
-2
分析：由题意易得向量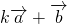
与
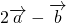的坐标，由向量共线的条件可得关于k的方程，解之即可．
解答：由已知可得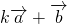=k（1，2）+（-3，2）=（k-3，2k+2），
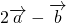=2（1，2）-（-3，2）=（5，2），
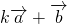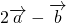因为向量与共线，
所以2（k-3）-5（2k+2）=0，
解得k=-2
故答案为：-2
点评：本题考查向量共线的坐标表示，属基础题．
分析：由题意易得向量
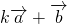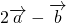与的坐标，由向量共线的条件可得关于k的方程，解之即可．解答：由已知可得
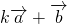=k（1，2）+（-3，2）=（k-3，2k+2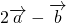），=2（1，2）-（-3，2）=（5，2），因为向量
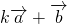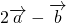与共线，所以2（k-3）-5（2k+2）=0，
解得k=-2
故答案为：-2
点评：本题考查向量共线的坐标表示，属基础题．
练习册系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
共线，则k= ．