题目内容
设
,
是两个非零向量,则下列结论不正确的是( )
| a |
| b |
分析:A.根据向量共线定理,即可判断出;
B.利用相等向量的模相等即可得出;
C.当
与
异向时,|
+
|<|
|+|
|=|
-
|,即可得出;
D.由于
与
为两个方向相同的向量,可得|
+
|=|
|+|
|.
B.利用相等向量的模相等即可得出;
C.当
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
D.由于
| a |
| b |
| a |
| b |
| a |
| b |
解答:解:A.根据向量共线定理,可知正确;
B.∵
=
,∴|
|=|
|;
C.当
与
异向时,|
+
|<|
|+|
|=|
-
|,因此不正确;
D.∵
与
为两个方向相同的向量,∴|
+
|=|
|+|
|,故正确.
综上可知:只有C不正确.
故选C.
B.∵
| a |
| b |
| a |
| b |
C.当
| a |
| b |
| a |
| b |
| a |
| b |
| a |
| b |
D.∵
| a |
| b |
| a |
| b |
| a |
| b |
综上可知:只有C不正确.
故选C.
点评:本题考查了向量形式的三角形不等式取等号的情况以及向量共线定理等基础知识与基本技能方法,属于基础题.

练习册系列答案
相关题目
 ,
, 是两个非零向量,则“向量
是两个非零向量,则“向量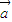 ,
,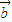 是两个非零向量,则“向量
是两个非零向量,则“向量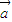 ,
,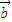 的夹角为锐角”是“函数f(x)=(x
的夹角为锐角”是“函数f(x)=(x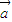 +
+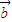 )•(
)•(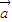 -x
-x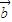 )的图象是一条开口向下的抛物线”的( )
)的图象是一条开口向下的抛物线”的( )