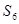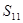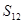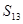题目内容
已知公差不为零的等差数列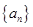 的前
的前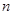 项和为
项和为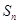 ,若
,若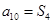 ,则
,则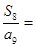 。
。
4
解析试题分析:根据题意,由于公差不为零的等差数列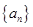 的前
的前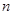 项和为
项和为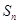 ,若
,若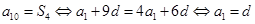 ,那么可知
,那么可知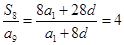 ,故可知答案为4.
,故可知答案为4.
考点:等差数列
点评:主要是考查了等差数列的前n项和以及通项公式 运用,属于基础题。

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
设等差数列{an}的前n项和为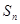 ,若
,若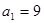 ,
,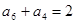 , 则当
, 则当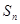 取最大值
取最大值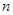 等于( )
等于( )
| A.4 | B.5 | C.6 | D.7 |
设等差数列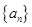 的前
的前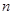 项和为
项和为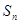 ,
,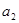 、
、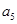 是方程
是方程 的两个根,
的两个根,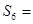 ( )
( )
A.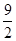 | B. | C.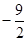 | D.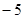 |
已知数列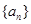 为等差数列,且
为等差数列,且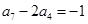 ,
, ,则公差
,则公差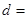 ( )
( )
| A.-2 | B.-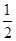 | C.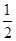 | D.2 |
若三位数 被7整除,且
被7整除,且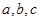 成公差非零的等差数列,则这样的整数共有( )个。
成公差非零的等差数列,则这样的整数共有( )个。
| A.4 | B.6 | C.7 | D.8 |
设 是等差数列,若
是等差数列,若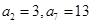 ,则数列
,则数列 前8项的和为( ).
前8项的和为( ).
| A.56 | B.64 | C.80 | D.128 |
在等差数列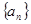 中,若
中,若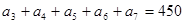 ,则
,则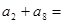 ( )
( )
| A.45 | B.75 | C.180 | D.300 |
设等差数列 的公差为
的公差为 ,若
,若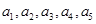 的方差为2,则
的方差为2,则 等于( )
等于( )
| A.1 | B.2 | C.±1 | D.±2 |
 的前
的前 项之和为
项之和为 ,若
,若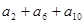 为一个确定的常数,则下列各数中也可以确定的是( )
为一个确定的常数,则下列各数中也可以确定的是( )