题目内容
已知数列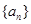 为等差数列,且
为等差数列,且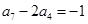 ,
, ,则公差
,则公差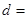 ( )
( )
| A.-2 | B.-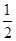 | C.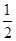 | D.2 |
B
解析试题分析:根据题意得 ,所以
,所以 ,又因为
,又因为 ,所以
,所以 .
.
考点:等差数列的通项公式.

练习册系列答案
相关题目
数列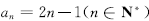 排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )
排出如图所示的三角形数阵,设2013位于数阵中第s行,第t列,则s+t=( )
| A.61 | B.62 | C.63 | D.64 |
已知数列{ }是公差为3的等差数列,且
}是公差为3的等差数列,且 成等比数列,则
成等比数列,则 等于( )
等于( )
| A.30 | B.27 | C.24 | D.33 |
等差数列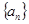 的前
的前 项和为
项和为 ,公差为
,公差为 ,已知
,已知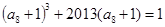 ,
,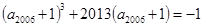 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. | B.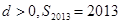 |
C.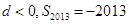 | D.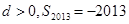 |
《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样的一道题目:把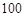 个面包分给
个面包分给 个人,使每人所得成等差数列,且使较大的三份之和的
个人,使每人所得成等差数列,且使较大的三份之和的 是较小的两份之和,则最小
是较小的两份之和,则最小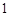 份为( )
份为( )
A. | B.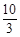 | C.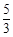 | D.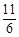 |
设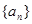 是等差数列,若
是等差数列,若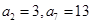 ,则数列
,则数列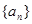 前8项的和为( )
前8项的和为( )
| A.128 | B.80 | C.64 | D.56 |
等差数列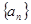 的公差
的公差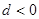 ,且
,且 ,则该数列的前
,则该数列的前 项和取得最大值时,
项和取得最大值时,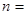
| A.6 | B.7 | C.6或7 | D.7或8 |
等差数列 前
前 项和为
项和为 ,
,  ,
, ,则
,则 =( )
=( )
| A.70 | B.80 | C.90 | D.100 |
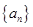 的前
的前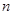 项和为
项和为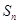 ,若
,若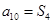 ,则
,则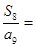 。
。