题目内容
设等差数列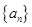 的前
的前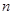 项和为
项和为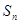 ,
,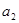 、
、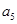 是方程
是方程 的两个根,
的两个根,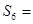 ( )
( )
A.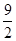 | B. | C.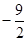 | D.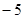 |
A
解析试题分析:由韦达定理可知 ,等差数列的性质知
,等差数列的性质知 ,根据等差数列的求和公式
,根据等差数列的求和公式 ,故选A.
,故选A.
考点:差数列的性质.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
设等差数列 的前
的前 项和为
项和为 ,若
,若 则
则 ( )
( )
| A.7 | B.6 | C.5 | D.4 |
已知 为等差数列,若
为等差数列,若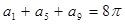 ,则
,则 的值为( )
的值为( )
A.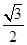 | B. | C.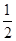 | D.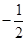 |
设等差数列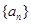 的前
的前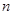 项和为
项和为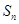 ,且
,且 ,
, ,则
,则 ( )
( )
| A.90 | B.100 | C.110 | D.120 |
等差数列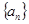 的前
的前 项和为
项和为 ,公差为
,公差为 ,已知
,已知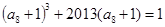 ,
,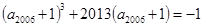 ,则下列结论正确的是( )
,则下列结论正确的是( )
A. | B.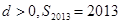 |
C.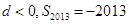 | D.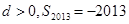 |
等差数列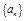 中的
中的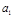 、
、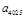 是函数
是函数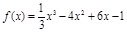 的极值点,则
的极值点,则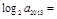 ( )
( )
A.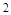 | B.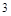 | C.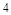 | D.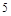 |
数列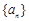 的前n项和为
的前n项和为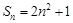 ,则an=( )
,则an=( )
| A.an=4n-2 |
| B.an=2n-1 |
C. |
D. |
已知等差数列 的值是( )
的值是( )
| A.15 | B.30 | C.31 | D.64 |
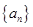 的前
的前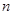 项和为
项和为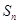 ,若
,若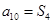 ,则
,则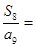 。
。