题目内容
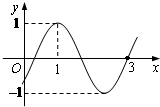 已知函数f(x)=sin(ωx+φ)(ω>0)的图象如右图所示,则f(2)=
已知函数f(x)=sin(ωx+φ)(ω>0)的图象如右图所示,则f(2)=考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由图可知
T=2,从而可求得ω,再由ω×1+φ=
+2kπ(k∈Z),可求得φ,于是可得y=f(x)的解析式,继而可求f(2)的值.
| 3 |
| 4 |
| π |
| 2 |
解答:
解:∵
T=3-1=2,
∴T=
=
,解得ω=
.
又ω×1+φ=
×1+φ=
+2kπ(k∈Z),
∴φ=-
+2kπ(k∈Z),
∴f(x)=sin(
x-
),
∴f(2)=sin(
-
)=-cos
=-
.
故答案为:-
.
| 3 |
| 4 |
∴T=
| 8 |
| 3 |
| 2π |
| ω |
| 3π |
| 4 |
又ω×1+φ=
| 3π |
| 4 |
| π |
| 2 |
∴φ=-
| π |
| 4 |
∴f(x)=sin(
| 3π |
| 4 |
| π |
| 4 |
∴f(2)=sin(
| 3π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| ||
| 2 |
故答案为:-
| ||
| 2 |
点评:本题考查由y=Asin(ωx+φ)的部分图象确定其解析式,确定ω、φ的值是关键,考查诱导公式与余弦函数的性质,考查转化思想.

练习册系列答案
 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案
相关题目
函数y=
+
的定义域是( )
| 1-x |
| x-1 |
| A、[1,+∞) | B、(-∞,1] |
| C、{1} | D、不能确定 |
 如图,OMN是半径为2,圆心角为120°的扇形,ABCD是扇形的内接矩形.
如图,OMN是半径为2,圆心角为120°的扇形,ABCD是扇形的内接矩形.
 如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数y=k
如图所示,某小区为美化环境,准备在小区内草坪的一侧修建一条直路OC;另一侧修建一条休闲大道,它的前一段OD是函数y=k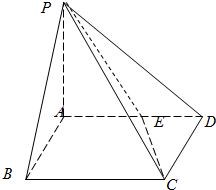 在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E为棱AD的中点.
在四棱锥P-ABCD中,PA⊥平面ABCD,底面ABCD为正方形,且PA=AD=2,E为棱AD的中点.