题目内容
已知等比数列{an}中,a3=4,a6=-32,求:
(1)a8;
(2)S10.
(1)a8;
(2)S10.
考点:等比数列的前n项和,等比数列的通项公式
专题:等差数列与等比数列
分析:由已知条件利用等比数列的通项公式求出首项和公比,由此能求出a8和S10.
解答:
解:(1)∵等比数列{an}中,a3=4,a6=-32,
∴
,
解得a1=1,q=-2,
∴a8=1×(-2)7=-128.
(2)∵a1=1,q=-2,
∴S10=
=-
=-341.
∴
|
解得a1=1,q=-2,
∴a8=1×(-2)7=-128.
(2)∵a1=1,q=-2,
∴S10=
| 1-(-2)10 |
| 1-(-2) |
| 1023 |
| 3 |
点评:本题考查数列的第8项和前10项和的求法,是基础题,解题时要认真审题,注意等比数列的性质的合理运用.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
如图框图属于( )
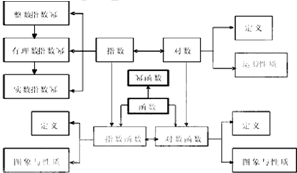

| A、程序框图 | B、工序流程图 |
| C、知识结构图 | D、组织结构图 |
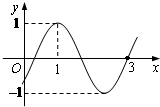 已知函数f(x)=sin(ωx+φ)(ω>0)的图象如右图所示,则f(2)=
已知函数f(x)=sin(ωx+φ)(ω>0)的图象如右图所示,则f(2)=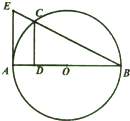 如图,EA是圆O的切线,割线EB交圆O于点C,C在直径AB上的射影为D,CD=2,BD=4,则EA=
如图,EA是圆O的切线,割线EB交圆O于点C,C在直径AB上的射影为D,CD=2,BD=4,则EA=