题目内容
已知实数a≥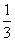 ,函数y=ex-ax是区间[-ln3,0)上的增函数,设函数f(x)=ax3-
,函数y=ex-ax是区间[-ln3,0)上的增函数,设函数f(x)=ax3-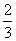 x,
x,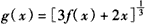 ,
,
(Ⅰ)求a的值并写出g(x)的表达式;
(Ⅱ)求证:当x>0时,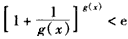 ;
;
(Ⅲ)设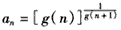 ,其中n∈N* ,问数列{an}中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由。
,其中n∈N* ,问数列{an}中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由。
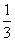 ,函数y=ex-ax是区间[-ln3,0)上的增函数,设函数f(x)=ax3-
,函数y=ex-ax是区间[-ln3,0)上的增函数,设函数f(x)=ax3-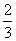 x,
x,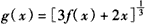 ,
,(Ⅰ)求a的值并写出g(x)的表达式;
(Ⅱ)求证:当x>0时,
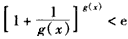 ;
;(Ⅲ)设
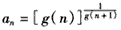 ,其中n∈N* ,问数列{an}中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由。
,其中n∈N* ,问数列{an}中是否存在相等的两项?若存在,求出所有相等的两项;若不存在,请说明理由。 (Ⅰ)解:∵函数y=ex-ax是区间[-ln3,0)上的增函数,
∴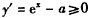 在[-ln3,0)上恒成立,
在[-ln3,0)上恒成立,
∴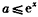 在x∈[-ln3,0)上恒成立,
在x∈[-ln3,0)上恒成立,
即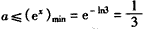 ,∴
,∴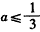 ,
,
又∵a≥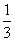 ,
,
∴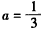 ,
,
∴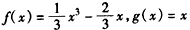 。
。
(Ⅱ)证明:当x>0时,原不等式等价于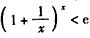 ,
,
两边取对数,即证: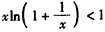 ,
,
即证: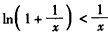 ,
,
设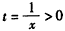 ,即证
,即证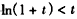 ,
,
事实上,设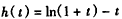 ,
,
则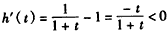 ,
,
∴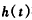 在
在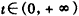 上单调递减,
上单调递减,
∴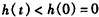 ,∴
,∴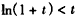 ,
,
∴原不等式成立。
(Ⅲ)解:∵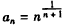 ,由(Ⅱ)可知,
,由(Ⅱ)可知,
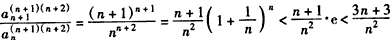 ,
,
令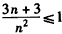 ,由
,由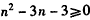 且n∈N*,得n≥4,
且n∈N*,得n≥4,
即n≥4时,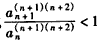 ,得
,得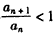 ,
,
∴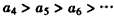 ,
,
又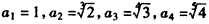 ,
,
∴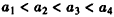 ,且
,且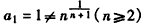 ,
,
∴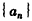 中只可能是
中只可能是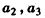 与后面的项相等,
与后面的项相等,
又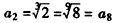 ,
,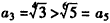 ,
,
∴数列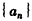 中存在唯一的两项相等
中存在唯一的两项相等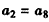 。
。
∴
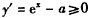 在[-ln3,0)上恒成立,
在[-ln3,0)上恒成立,∴
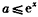 在x∈[-ln3,0)上恒成立,
在x∈[-ln3,0)上恒成立,即
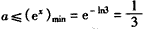 ,∴
,∴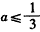 ,
,又∵a≥
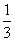 ,
,∴
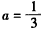 ,
,∴
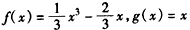 。
。(Ⅱ)证明:当x>0时,原不等式等价于
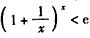 ,
,两边取对数,即证:
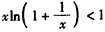 ,
,即证:
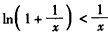 ,
,设
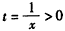 ,即证
,即证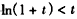 ,
,事实上,设
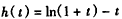 ,
,则
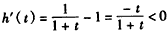 ,
,∴
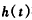 在
在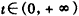 上单调递减,
上单调递减,∴
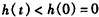 ,∴
,∴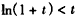 ,
,∴原不等式成立。
(Ⅲ)解:∵
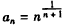 ,由(Ⅱ)可知,
,由(Ⅱ)可知,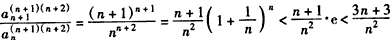 ,
,令
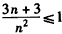 ,由
,由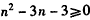 且n∈N*,得n≥4,
且n∈N*,得n≥4,即n≥4时,
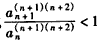 ,得
,得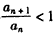 ,
,∴
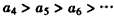 ,
,又
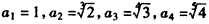 ,
,∴
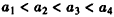 ,且
,且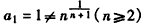 ,
,∴
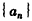 中只可能是
中只可能是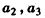 与后面的项相等,
与后面的项相等,又
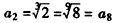 ,
,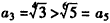 ,
,∴数列
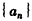 中存在唯一的两项相等
中存在唯一的两项相等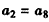 。
。
练习册系列答案
相关题目