题目内容
设函数 .
.
(Ⅰ)求函数 的极值;
的极值;
(Ⅱ)是否存在 ,使得
,使得 在该区间上的值域为
在该区间上的值域为 ?若存在,求出
?若存在,求出 的值;若不存在,说明理由.
的值;若不存在,说明理由.
(Ⅰ)
 在
在 上单调递增,
上单调递增, 上单调递减.
上单调递减.

(Ⅱ) ,
,
若 则
则 ,故有
,故有
构造 ,
,
 为唯一解.
为唯一解.
若 ,则
,则 即
即 或
或
① 时
时  前面已证至多一解,不存
前面已证至多一解,不存
在满足条件的 ;
;
② 时,
时, ,相除得
,相除得
记  ,
,
则  ,
,
 在
在 递增,
递增, 递减,由
递减,由

此时 矛盾.
矛盾.
综上所述,满足条件的 为
为

练习册系列答案
 步步高达标卷系列答案
步步高达标卷系列答案
相关题目
 满足
满足 若
若 恒成立,则实数
恒成立,则实数 的最大值是 .
的最大值是 . 的两条渐近线为
的两条渐近线为 ,过右焦点
,过右焦点 作垂直
作垂直 的直线交
的直线交 两点.若
两点.若 成等差数列,则双曲线的离心率为
成等差数列,则双曲线的离心率为 (B)
(B) (C)
(C) (D)
(D)
 为
为 的外心,
的外心, .若
.若 , 则
, 则 = .
= . ,过椭圆
,过椭圆 上一点
上一点 作倾斜角互补的两条直线
作倾斜角互补的两条直线 、
、 ,分别交椭圆
,分别交椭圆 、
、 两点.则直线
两点.则直线 的斜率为 .
的斜率为 . 米有两个垂直于水平地面的高塔
米有两个垂直于水平地面的高塔 和
和 ,两塔底
,两塔底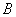 、
、 的中点为
的中点为 ,已知
,已知 米,
米, 米,则
米,则 的值是 .
的值是 . 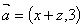 ,
,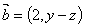 ,且
,且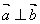 ,若实数
,若实数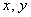 满足不等式
满足不等式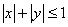 ,则实数
,则实数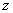 的取值范围为
的取值范围为 C.
C.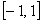 D.
D.