题目内容
设数列{an}的各项均为正数,其前n项的和为Sn,对于任意正整数m,n, 恒成立.
恒成立.
(1)若a1=1,求a2,a3,a4及数列{an}的通项公式;
(2)若a4=a2(a1+a2+1),求证:数列{an}成等比数列.
解(1)由 得
得 .
.
令m=1,得 ①
①
令m=2,得 ②
②
②÷①得: (n∈N*).记
(n∈N*).记 ,
,
则数列{1+Sn} (n≥2,n∈N*)是公比为q的等比数列.
∴ (n≥2,n∈N*)③.
(n≥2,n∈N*)③.
n≥3时, ④.
④.
③-④得, (n≥3,n∈N*).
(n≥3,n∈N*).
在 中,令m=n=1,得
中,令m=n=1,得 .
.
∴ .
.
则1+S2=2a2,∴a2=1+a1.
∵a1=1,∴a2=2.
在 中,令m=1,n=2,得
中,令m=1,n=2,得 .
.
则 ⑤
⑤
在 中,令m=2,n=1,得
中,令m=2,n=1,得
则 ⑥.
⑥.
由⑤,⑥,解得a3=4,a4=8.
则q=2,由 (n≥3,n∈N*),
(n≥3,n∈N*),
得:
∵a1=1,a2=2也适合上式,∴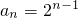 .
.
(2)在 中,令m=2,n=2,得
中,令m=2,n=2,得
则1+S4=2a4,∴1+S3=a4.
在 中,令m=1,n=2,得
中,令m=1,n=2,得 .
.
则 ,∴
,∴ .
.
则a4=4a2,∴ .
.
代入 (n≥3,n∈N*),
(n≥3,n∈N*),
得 (n≥3,n∈N*).
(n≥3,n∈N*).
由条件a4=a2(a1+a2+1),得a1+a2+1=4.
∵a2=a1+1,a1=1,∴a2=2.
则
∵a1=1,a2=2上式也成立,
∴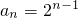 (n∈N*).
(n∈N*).
故数列{an}成等比数列.
分析:(1)由给出的递推式分别取m=1,m=2得到两个关系式,两式作比后可以证明数列{1+Sn}是一个等比数列,由等比数列的通项公式得到Sn的表达式,模仿该式再写一个关系式,两式作差后进一步得到一个关于a2和S2的关系式,然后把a1代入即可求得a2的值,在分别取m=1,n=2;m=2,n=1代入原递推式,得到关于a3,a4的方程后可求解a3,a4则数列{an}的通项公式可求;
(2)在(1)的基础上,取m=n=2得关系式,结合m=1,n=2得到的关系式可求出q= =2.最后结合题目给出的条件,a4=a2(a1+a2+1)证出数列{an}成等比数列.
=2.最后结合题目给出的条件,a4=a2(a1+a2+1)证出数列{an}成等比数列.
点评:本题考查了等比关系的确定,考查了等差数列和等比数列的综合,训练了学生的灵活变形能力和对繁杂问题的计算能力,属中高档题.
 得
得 .
.令m=1,得
 ①
①令m=2,得
 ②
②②÷①得:
 (n∈N*).记
(n∈N*).记 ,
,则数列{1+Sn} (n≥2,n∈N*)是公比为q的等比数列.
∴
 (n≥2,n∈N*)③.
(n≥2,n∈N*)③.n≥3时,
 ④.
④.③-④得,
 (n≥3,n∈N*).
(n≥3,n∈N*).在
 中,令m=n=1,得
中,令m=n=1,得 .
.∴
 .
.则1+S2=2a2,∴a2=1+a1.
∵a1=1,∴a2=2.
在
 中,令m=1,n=2,得
中,令m=1,n=2,得 .
.则
 ⑤
⑤在
 中,令m=2,n=1,得
中,令m=2,n=1,得
则
 ⑥.
⑥.由⑤,⑥,解得a3=4,a4=8.
则q=2,由
 (n≥3,n∈N*),
(n≥3,n∈N*),得:

∵a1=1,a2=2也适合上式,∴
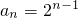 .
.(2)在
 中,令m=2,n=2,得
中,令m=2,n=2,得
则1+S4=2a4,∴1+S3=a4.
在
 中,令m=1,n=2,得
中,令m=1,n=2,得 .
.则
 ,∴
,∴ .
.则a4=4a2,∴
 .
.代入
 (n≥3,n∈N*),
(n≥3,n∈N*),得
 (n≥3,n∈N*).
(n≥3,n∈N*).由条件a4=a2(a1+a2+1),得a1+a2+1=4.
∵a2=a1+1,a1=1,∴a2=2.
则

∵a1=1,a2=2上式也成立,
∴
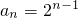 (n∈N*).
(n∈N*).故数列{an}成等比数列.
分析:(1)由给出的递推式分别取m=1,m=2得到两个关系式,两式作比后可以证明数列{1+Sn}是一个等比数列,由等比数列的通项公式得到Sn的表达式,模仿该式再写一个关系式,两式作差后进一步得到一个关于a2和S2的关系式,然后把a1代入即可求得a2的值,在分别取m=1,n=2;m=2,n=1代入原递推式,得到关于a3,a4的方程后可求解a3,a4则数列{an}的通项公式可求;
(2)在(1)的基础上,取m=n=2得关系式,结合m=1,n=2得到的关系式可求出q=
 =2.最后结合题目给出的条件,a4=a2(a1+a2+1)证出数列{an}成等比数列.
=2.最后结合题目给出的条件,a4=a2(a1+a2+1)证出数列{an}成等比数列.点评:本题考查了等比关系的确定,考查了等差数列和等比数列的综合,训练了学生的灵活变形能力和对繁杂问题的计算能力,属中高档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目