题目内容
(本小题满分14分)、
已知函数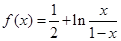 .
.
(Ⅰ)求证:存在定点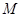 ,使得函数
,使得函数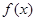 图象上任意一点
图象上任意一点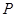 关于
关于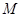 点对称的点
点对称的点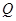 也在函数
也在函数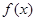 的图象上,并求出点
的图象上,并求出点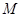 的坐标;
的坐标;
(Ⅱ)定义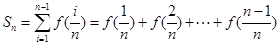 ,其中
,其中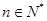 且
且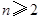 ,求
,求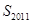 ;
;
(Ⅲ)对于(Ⅱ)中的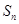 ,求证:对于任意
,求证:对于任意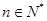 都有
都有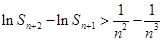 .
.
已知函数
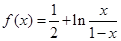 .
.(Ⅰ)求证:存在定点
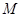 ,使得函数
,使得函数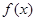 图象上任意一点
图象上任意一点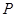 关于
关于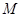 点对称的点
点对称的点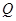 也在函数
也在函数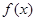 的图象上,并求出点
的图象上,并求出点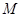 的坐标;
的坐标;(Ⅱ)定义
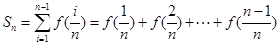 ,其中
,其中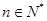 且
且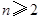 ,求
,求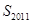 ;
;(Ⅲ)对于(Ⅱ)中的
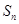 ,求证:对于任意
,求证:对于任意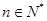 都有
都有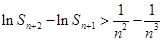 .
..解:(Ⅰ)显然函数定义域为(0,1). 设点M的坐标为(a, b),
则由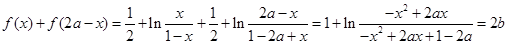
对于 恒成立,于是
恒成立,于是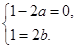 解得
解得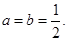
所以存在定点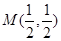 ,使得函数f(x)的图象上任意一点P关于M点对称的点Q也在函数f(x)的图象上. 4分
,使得函数f(x)的图象上任意一点P关于M点对称的点Q也在函数f(x)的图象上. 4分
(Ⅱ)由(Ⅰ)得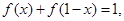
∵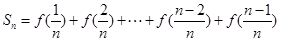 ……①
……①
∴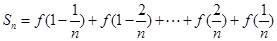 ②
②
①+②,得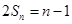 ,∴
,∴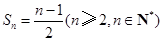 ,故
,故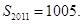 8分
8分
(Ⅲ)当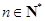 时,由(Ⅱ)知
时,由(Ⅱ)知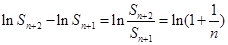 ,
,
于是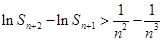 等价于
等价于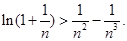 0分
0分
令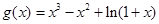 ,则
,则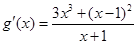 ,
,
∴当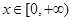 时,
时,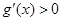 ,即函数
,即函数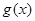 在
在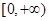 上单调递增,又g(0)=0.
上单调递增,又g(0)=0.
于是,当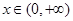 时,恒有
时,恒有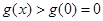 ,即
,即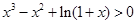 恒成立. …12分
恒成立. …12分
故当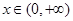 时,有
时,有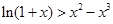 成立,取
成立,取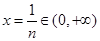 ,
,
则有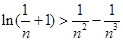 成立. 14分
成立. 14分
则由
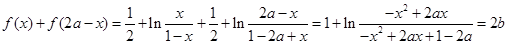
对于
 恒成立,于是
恒成立,于是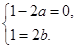 解得
解得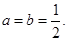
所以存在定点
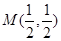 ,使得函数f(x)的图象上任意一点P关于M点对称的点Q也在函数f(x)的图象上. 4分
,使得函数f(x)的图象上任意一点P关于M点对称的点Q也在函数f(x)的图象上. 4分(Ⅱ)由(Ⅰ)得
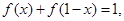
∵
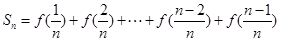 ……①
……①∴
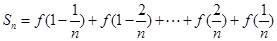 ②
②①+②,得
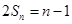 ,∴
,∴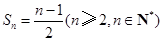 ,故
,故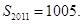 8分
8分(Ⅲ)当
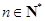 时,由(Ⅱ)知
时,由(Ⅱ)知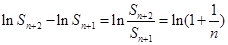 ,
,于是
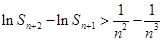 等价于
等价于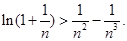 0分
0分令
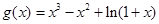 ,则
,则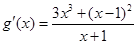 ,
,∴当
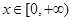 时,
时,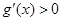 ,即函数
,即函数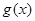 在
在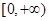 上单调递增,又g(0)=0.
上单调递增,又g(0)=0.于是,当
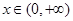 时,恒有
时,恒有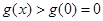 ,即
,即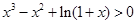 恒成立. …12分
恒成立. …12分故当
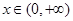 时,有
时,有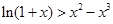 成立,取
成立,取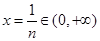 ,
,则有
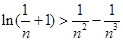 成立. 14分
成立. 14分略

练习册系列答案
相关题目
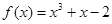 在
在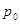 处的切线垂直于直线
处的切线垂直于直线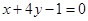 ,则
,则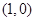 B
B 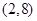 C
C 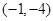 D
D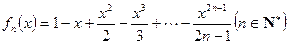 .
.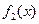 的单调性;
的单调性;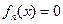 的实数解的个数,并加以证明.
的实数解的个数,并加以证明.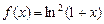
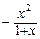 .
.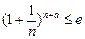 对任意的
对任意的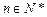 都成立(其中e是自然对数的底数),求a的最大值。
都成立(其中e是自然对数的底数),求a的最大值。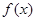 是
是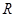 上最小正周期为2的周期函数,且当
上最小正周期为2的周期函数,且当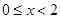 时,
时,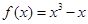 ,则函数
,则函数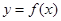 的图象在区间[0,6]上与
的图象在区间[0,6]上与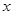 轴的交点的个数为( )
轴的交点的个数为( )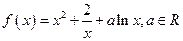
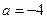 ,求函数
,求函数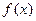 的单调区间;
的单调区间;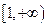 上单调递增,求实数
上单调递增,求实数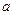 的取值范围
的取值范围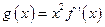 ,若
,若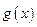 的最小值是
的最小值是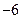 ,求函数
,求函数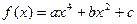 的图象经过点
的图象经过点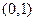 ,且在
,且在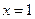 处的切线方程是
处的切线方程是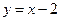
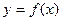 的解析式;
的解析式;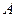 、
、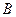 为椭圆
为椭圆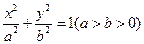 和双曲线
和双曲线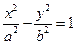 的公共顶点,
的公共顶点,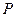 、
、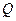 分别为双曲线和椭圆上不同于
分别为双曲线和椭圆上不同于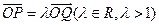 .设
.设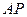 、
、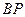 、
、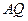 、
、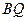 的斜率分别为
的斜率分别为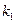 、
、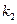 、
、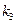 、
、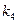 .
.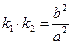 ;
;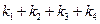 的值;
的值;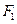 、
、 分别为双曲线和椭圆的右焦点,若
分别为双曲线和椭圆的右焦点,若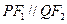 ,求
,求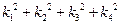 的值.
的值.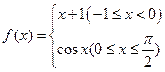 的图像与
的图像与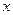 轴围成的封闭图形的面积为
轴围成的封闭图形的面积为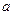 ,则
,则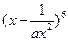 的展开式中的常数项为( )
的展开式中的常数项为( )