复数i+i2+i3+-+i2012+i2013的值为i．题目和参考答案——青夏教育精英家教网—

题目内容

7．复数i+i²+i³+…+i²⁰¹²+i²⁰¹³的值为i．

分析利用等比数列的前n项和公式以及复数单位i²=-1，计算即可．

解答解：复数i+i²+i³+…+i²⁰¹²+i²⁰¹³=$\frac{i（1{-i}^{2013}）}{1-i}$
=$\frac{i{-i}^{2014}}{1-i}$
=$\frac{i+1}{1-i}$
=$\frac{{（1+i）}^{2}}{1{-i}^{2}}$
=i．
故答案为：i．

点评本题考查了等比数列的前n项和公式与复数单位i的运算问题，是基础题．

练习册系列答案

相关题目

14．（a+bi）（a-bi）（-a+bi）（-a-bi）等于（　　）

a²+b²

a²-b²

18．若函数f（x）=$\frac{1}{2}$（x-1）²+a的定义域和值域都是[1，b]（b＞1），则a+b的值等于（　　）

15．已知x∈N，则方程x²+x-2=0的解集用列举法可表示为{1}．

2．在矩形ABCD中，AB=2，AD=1，E为CD的中点，将△ADE沿AE折起，使平面ADE⊥平面ABCE，得到几何体D-ABCE，M点是此时BD的中点．

（1）求异面直BE和CM所成角的大小；
（2）求BD与平面ADE所成角的余弦值．

12．定义点P（x₀，y₀）到直线l：ax+by+c=0（a²+b²≠0）的有向距离为：$d=\frac{{a{x_0}+b{y_0}+c}}{{\sqrt{{a^2}+{b^2}}}}$．已知点P₁、P₂到直线l的有向距离分别是d₁、d₂．以下命题正确的是（　　）

	A．	若d₁=d₂=1，则直线P₁P₂与直线l平行
	B．	若d₁=1，d₂=-1，则直线P₁P₂与直线l垂直
	C．	若d₁+d₂=0，则直线P₁P₂与直线l垂直
	D．	若d₁•d₂≤0，则直线P₁P₂与直线l相交

19．

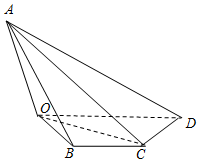如图，四棱锥A-OBCD中，已知平面AOC⊥面OBCD，AO=2$\sqrt{3}$，OB=BC=2，CD=4，∠OBC=∠BCD=120°．
（I）求证：平面ACD⊥平面AOC；
（II）直线AO与平面OBCD所成角为60°，求二面角A-BC-D的平面角的正切值．

16．若复数z满足zi=2-3i（i是虚数单位），则复数z的共轭复数为（　　）

17．若函数f（x）=5cos（wx+φ）对任意实数x，都有$f（\frac{π}{3}+x）=f（\frac{π}{3}-x）$，函数g（x）=4sin（wx+φ）+1则$g（\frac{π}{3}）$=（　　）

试题分类