题目内容
定义在R上的偶函数R满足,x>0时,f(x)=x+
.
(1)求x<0时,f(x)的解析式;
(2)求证:函数f(x)在区间(0,2)上递减.
| 4 |
| x |
(1)求x<0时,f(x)的解析式;
(2)求证:函数f(x)在区间(0,2)上递减.
(1)当x<0时,-x>0,
因为x>0时,f(x)=x+
,
所以 f(-x)=-x-
,
因为该函数是偶函数,所以f(x)=-x-
.
(2)任取x1,x2∈(0,2),且x1<x2,
所以f(x1)-f(x2)=-x1-
+x2+
=
,
因为0<x1<x2<2,
所以4>x1x2>0,x1-x2<0,
所以f(x1)-f(x2)>0,即f(x1)>f(x2),
所以函数f(x)在区间(0,2)上递减.
因为x>0时,f(x)=x+
| 4 |
| x |
所以 f(-x)=-x-
| 4 |
| x |
因为该函数是偶函数,所以f(x)=-x-
| 4 |
| x |
(2)任取x1,x2∈(0,2),且x1<x2,
所以f(x1)-f(x2)=-x1-
| 4 |
| x1 |
| 4 |
| x2 |
| (x1-x2)(x1x2-4) |
| x1x2 |
因为0<x1<x2<2,
所以4>x1x2>0,x1-x2<0,
所以f(x1)-f(x2)>0,即f(x1)>f(x2),
所以函数f(x)在区间(0,2)上递减.

练习册系列答案
相关题目
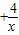 .
. R),
R), =
2x2+3x-1,h (x)为f
(x)、g(x)在R上生成的一个二次函数.
=
2x2+3x-1,h (x)为f
(x)、g(x)在R上生成的一个二次函数. ,若h (x)为偶函数,求
,若h (x)为偶函数,求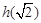 ;
; ,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;
,若h (x)同时也是g(x)、l(x) 在R上生成的一个函数,求a+b的最小值;