题目内容
定义在R上的偶函数R满足，x＞0时，f（x）=x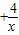
．（1）求x＜0时，f（x）的解析式；
（2）求证：函数f（x）在区间（0，2）上递减．
【答案】分析：（1）利用所求函数的区间与已知区间是对称的，再结合奇偶性求解；（2）利用定义判断函数的单调性．
解答：解：（1）当x＜0时，-x＞0，
因为x＞0时，
，
所以
，
因为该函数是偶函数，所以
．
（2）任取x1，x2∈（0，2），且x1＜x2，
所以
=
，
因为0＜x1＜x2＜2，
所以4＞x1x2＞0，x1-x2＜0，
所以f（x1）-f（x2）＞0，即f（x1）＞f（x2），
所以函数f（x）在区间（0，2）上递减．
点评：本题考察利用函数奇偶性求函数解析式和函数单调性的判断，属基础题．
解答：解：（1）当x＜0时，-x＞0，
因为x＞0时，
，所以
，因为该函数是偶函数，所以
．（2）任取x1，x2∈（0，2），且x1＜x2，
所以
=，因为0＜x1＜x2＜2，
所以4＞x1x2＞0，x1-x2＜0，
所以f（x1）-f（x2）＞0，即f（x1）＞f（x2），
所以函数f（x）在区间（0，2）上递减．
点评：本题考察利用函数奇偶性求函数解析式和函数单调性的判断，属基础题．
练习册系列答案
相关题目
R)，
=
2x2+3x-1，h (x)为f
(x)、g(x)在R上生成的一个二次函数.
，若h (x)为偶函数，求
；
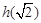，若h (x)同时也是g(x)、l(x) 在R上生成的一个函数，求a+b的最小值；