Question

【题目】已知抛物线()的焦点为，以抛物线上一动点为圆心的圆经过点F.若圆的面积最小值为.

(Ⅰ)求的值；

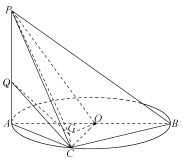
(Ⅱ)当点的横坐标为1且位于第一象限时，过作抛物线的两条弦，且满足.若直线AB恰好与圆相切，求直线AB的方程.

Answer 1

【答案】(1);(2).

【解析】分析：(Ⅰ)由抛物线的性质知，当圆心位于抛物线的顶点时，圆的面积最小，由可得的值；(Ⅱ)依横坐标相等可得，轴，，设()，则直线的方程为，代入抛物线的方程得，利用韦达定理求出的坐标，同理求出的坐标，求出的斜率为定值，设直线的方程为，由圆心到直线的距离等于半径，列方程解得，从而可得直线的方程.

详解：(Ⅰ)由抛物线的性质知，当圆心位于抛物线的顶点时，圆的面积最小，

此时圆的半径为，∴，解得.

(Ⅱ)依题意得，点的坐标为(1，2)，圆的半径为2.

由(1，0)知，轴.

由知，弦，所在直线的倾斜角互补，∴.

设()，则直线的方程为，∴，

代入抛物线的方程得，，∴，

∴.

将换成，得，

∴.

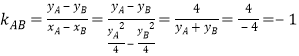设直线的方程为，即.

由直线与圆相切得，，解得.

经检验不符合要求，故舍去.

∴所求直线的方程为.