题目内容
【题目】已知函数![]()
![]() ,在一个周期内的图象如下图所示.
,在一个周期内的图象如下图所示.
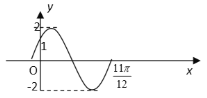
(1)求函数的解析式;
(2)设![]() ,且方程
,且方程![]() 有两个不同的实数根,求实数m的取值范围和这两个根的和.
有两个不同的实数根,求实数m的取值范围和这两个根的和.
【答案】(1)![]() ,(2)
,(2)![]() 或
或![]() ;当
;当![]() 时,两根之和
时,两根之和![]() ;当
;当![]() )时,两根之和
)时,两根之和![]() .
.
【解析】
(1)观察图象可得:![]() ,根据
,根据![]() 求出
求出![]() ,再根据
,再根据![]() 可得
可得![]() .可得解;(2)如图所示,
.可得解;(2)如图所示,![]() .作出直线
.作出直线![]() .方程
.方程![]() 有两个不同的实数根转化为:函数
有两个不同的实数根转化为:函数![]() .与函数
.与函数![]() 图象交点的个数.利用图象的对称性质即可得出.
图象交点的个数.利用图象的对称性质即可得出.
(1)观察图象可得:![]() ,
,
因为f(0)=1,所以![]() .
.
因为![]() ,
,
由图象结合五点法可知,![]() 对应于函数y=sinx的点
对应于函数y=sinx的点![]() ,
,
所以![]()
![]() .
.
(2)如图所示,![]() .
.
作出直线![]() .
.
方程![]() 有两个不同的实数根转化为:函数
有两个不同的实数根转化为:函数![]() .
.
与函数![]() 图象交点的个数.
图象交点的个数.
可知:当![]() 时,此时两个函数图象有两个交点,关于直线
时,此时两个函数图象有两个交点,关于直线![]() 对称,两根和为
对称,两根和为![]() .
.
当![]() 时,此时两个函数图象有两个交点,关于直线
时,此时两个函数图象有两个交点,关于直线![]() 对称,两根和为
对称,两根和为![]() .
.


练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目

