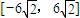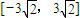题目内容
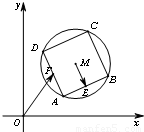
 如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,
如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E为边AB的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时, 的最大值是________.
的最大值是________.
6
分析:由题意可得 =
= =
= +
+ .由 ME⊥MF,可得
.由 ME⊥MF,可得 =0,从而
=0,从而  =
= .求得
.求得  =6cos<
=6cos<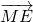 ,
, >,从而求得
>,从而求得 的最大值.
的最大值.
解答:由题意可得 =
= ,∴
,∴ =
= =
= +
+ .
.
∵ME⊥MF,∴ =0,∴
=0,∴ =
= .
.
∵ME= ,OM=3
,OM=3 ,∴
,∴ =
= •3
•3 •cos<
•cos<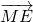 ,
, >=6cos<
>=6cos<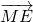 ,
, >,
>,
即 =6cos<
=6cos<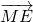 ,
, >,故
>,故  的最大值是大为6,
的最大值是大为6,
故答案为 6.
点评:本题主要考查两个向量的数量积的定义,两个向量的加减法的法则,以及其几何意义,余弦函数的值域,属于中档题.
分析:由题意可得
 =
= =
= +
+ .由 ME⊥MF,可得
.由 ME⊥MF,可得 =0,从而
=0,从而  =
= .求得
.求得  =6cos<
=6cos<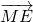 ,
, >,从而求得
>,从而求得 的最大值.
的最大值.解答:由题意可得
 =
= ,∴
,∴ =
= =
= +
+ .
.∵ME⊥MF,∴
 =0,∴
=0,∴ =
= .
.∵ME=
 ,OM=3
,OM=3 ,∴
,∴ =
= •3
•3 •cos<
•cos<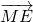 ,
, >=6cos<
>=6cos<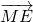 ,
, >,
>,即
 =6cos<
=6cos<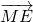 ,
, >,故
>,故  的最大值是大为6,
的最大值是大为6,故答案为 6.
点评:本题主要考查两个向量的数量积的定义,两个向量的加减法的法则,以及其几何意义,余弦函数的值域,属于中档题.

练习册系列答案
 新思维寒假作业系列答案
新思维寒假作业系列答案
相关题目
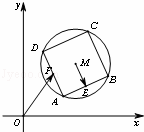
如图,已知圆M:(x﹣3)2+(y﹣3)2=4,四边形 ABCD为圆M的内接正方形,E,F分别为边AB,AD的中点,当正方形ABCD绕圆心M转动时,![]() 的取值范围是( )
的取值范围是( )
|
| A. |
| B. | [﹣6,6] | C. |
| D. | [﹣4,4] |
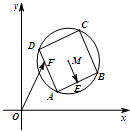 (2013•丽水一模)如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E、F分别为AB、AD的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,
(2013•丽水一模)如图,已知圆M:(x-3)2+(y-3)2=4,四边形ABCD为圆M的内接正方形,E、F分别为AB、AD的中点,当正方形ABCD绕圆心M转动,同时点F在边AD上运动时,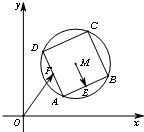 (2013•丽水一模)如图,已知圆M:(x-3)2+(y-3)2=4,四边形 ABCD为圆M的内接正方形,E,F分别为边AB,AD的中点,当正方形ABCD绕圆心M转动时,
(2013•丽水一模)如图,已知圆M:(x-3)2+(y-3)2=4,四边形 ABCD为圆M的内接正方形,E,F分别为边AB,AD的中点,当正方形ABCD绕圆心M转动时,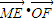 的取值范围是( )
的取值范围是( )
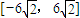

 的取值范围是( )
的取值范围是( )