题目内容
已知函数g(x)= -
- sinxcos-
sinxcos- x的图象按向量
x的图象按向量 =(-
=(- ,
, )平移得到函数f(x)=acos2(x+
)平移得到函数f(x)=acos2(x+ )+b的图象.
)+b的图象.
(1)求实数a、b的值;
(2)设函数φ(x)=g(x)- f(x),x∈[0,
f(x),x∈[0, ],求函数φ(x)的单调递增区间和最值.
],求函数φ(x)的单调递增区间和最值.
解:(1)依题意按向量 平移g(x)得f(x)-
平移g(x)得f(x)- =
= sin[2(x+
sin[2(x+ )+
)+ ]
]
得f(x)=- sin(2x+
sin(2x+ )+
)+ ,
,
又f(x)=acos2(x+ )+b=-
)+b=- sin(2x+
sin(2x+ )+
)+ +b,
+b,
比较得a=1,b=0;
(2)φ(x)=g(x)- f(x)
f(x)
= sin(2x+
sin(2x+ )-
)- cos(2x+
cos(2x+ )-
)-
=sin(2x+ )-
)- ,
,
∴φ(x)的单调增区间为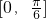 ,值域为[-
,值域为[-
分析:(1)由题意按向量 平移g(x),确定平移后的解析式,与函数f(x)=acos2(x+
平移g(x),确定平移后的解析式,与函数f(x)=acos2(x+ )+b的图象相同,比较系数,求实数a、b的值;
)+b的图象相同,比较系数,求实数a、b的值;
(2)化简函数φ(x)=g(x)- f(x)的表达式,为一个角的一个三角函数的形式,求函数φ(x)的单调递增区间,根据x∈[0,
f(x)的表达式,为一个角的一个三角函数的形式,求函数φ(x)的单调递增区间,根据x∈[0, ],求出它的最值.
],求出它的最值.
点评:本题考查函数y=Asin(ωx+φ)的图象变换,正弦函数的单调性,三角函数的最值,考查计算能力,逻辑思维能力,是基础题.
 平移g(x)得f(x)-
平移g(x)得f(x)- =
= sin[2(x+
sin[2(x+ )+
)+ ]
]得f(x)=-
 sin(2x+
sin(2x+ )+
)+ ,
,又f(x)=acos2(x+
 )+b=-
)+b=- sin(2x+
sin(2x+ )+
)+ +b,
+b,比较得a=1,b=0;
(2)φ(x)=g(x)-
 f(x)
f(x)=
 sin(2x+
sin(2x+ )-
)- cos(2x+
cos(2x+ )-
)-
=sin(2x+
 )-
)- ,
,∴φ(x)的单调增区间为
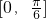 ,值域为[-
,值域为[-
分析:(1)由题意按向量
 平移g(x),确定平移后的解析式,与函数f(x)=acos2(x+
平移g(x),确定平移后的解析式,与函数f(x)=acos2(x+ )+b的图象相同,比较系数,求实数a、b的值;
)+b的图象相同,比较系数,求实数a、b的值;(2)化简函数φ(x)=g(x)-
 f(x)的表达式,为一个角的一个三角函数的形式,求函数φ(x)的单调递增区间,根据x∈[0,
f(x)的表达式,为一个角的一个三角函数的形式,求函数φ(x)的单调递增区间,根据x∈[0, ],求出它的最值.
],求出它的最值.点评:本题考查函数y=Asin(ωx+φ)的图象变换,正弦函数的单调性,三角函数的最值,考查计算能力,逻辑思维能力,是基础题.

练习册系列答案
相关题目