题目内容
已知样本9,10,11,x,y的平均数是10,标准差的最小值是
.
| ||
| 5 |
| ||
| 5 |
分析:根据方差和平均数公式,列出方程得出x、y的和为定值,再利用基本不等式求出方差的最小值,最后开方即得标准差的最小值.注意运算正确性.
解答:解:∵样本9,10,11,x,y的平均数是10,
∴(9+10+11+x+y)÷5=10,
∴x+y=20
方差=
[1+0+1+(x-10)2+(y-10)2]
=
+
[(x-10)2+(y-10)2]≥
+
×
=
,
∴方差的最小值是
,
∴标准差的最小值是
,
故答案为:
.
∴(9+10+11+x+y)÷5=10,
∴x+y=20
方差=
| 1 |
| 5 |
=
| 2 |
| 5 |
| 1 |
| 5 |
| 2 |
| 5 |
| 1 |
| 5 |
| (x-10+y-10)2 |
| 2 |
| 2 |
| 5 |
∴方差的最小值是
| 2 |
| 5 |
∴标准差的最小值是
| ||
| 5 |
故答案为:
| ||
| 5 |
点评:本小题主要考查平均数、极差、方差与标准差、基本不等式等基础知识,考查运算求解能力,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
 ,则xy=96;
,则xy=96;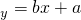 所表示的直线必恒经过点(1.5,2);
所表示的直线必恒经过点(1.5,2); ”的概率为
”的概率为 .
. ,则xy=96;
,则xy=96; 所表示的直线必恒经过点(1.5,2);
所表示的直线必恒经过点(1.5,2); ”的概率为
”的概率为 .
.