题目内容
下列说法正确的有________.(把所有正确说法的序号都填在横线上);
①抛掷两枚硬币,出现“两枚都是正面朝上”、“两枚都是反面朝上”、“恰好一枚硬币正面朝上”的概率一样大;
②已知样本9,10,11,x,y的平均数是10,标准差是 ,则xy=96;
,则xy=96;
③已知两相关变量x,y之间的一组数据如下:(0,8),(1,2),(2,6),(3,4),则线性回归方程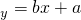 所表示的直线必恒经过点(1.5,2);
所表示的直线必恒经过点(1.5,2);
④向面积为S的△ABC内任投一点P,则随机事件”△PBC的面积小于 ”的概率为
”的概率为 .
.
②④
分析:①抛掷两枚硬币,出现“两枚都是正面朝上”的概率=“两枚都是反面朝上”的概率= ,“恰好一枚硬币正面朝上”的概率=
,“恰好一枚硬币正面朝上”的概率= .故①不正确;②由样本9,10,11,x,y的平均数是10,知x+y=20.由标准差是
.故①不正确;②由样本9,10,11,x,y的平均数是10,知x+y=20.由标准差是 ,知x2+y2-20(x+y)+200=8,所以xy=96.故②成立;③线性回归方程
,知x2+y2-20(x+y)+200=8,所以xy=96.故②成立;③线性回归方程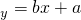 所表示的直线必恒经过点(1.5,5).故③不成立;④在AB上取M使
所表示的直线必恒经过点(1.5,5).故③不成立;④在AB上取M使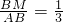 ,即
,即 ,过M作MN‖BC交AC于N,△ABC∽△AMN,由S在△ANM中不满足要求,S在梯形MNCB中满足要求,知概率=
,过M作MN‖BC交AC于N,△ABC∽△AMN,由S在△ANM中不满足要求,S在梯形MNCB中满足要求,知概率=
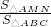 =
= .故④成立.
.故④成立.
解答:①抛掷两枚硬币,出现“两枚都是正面朝上”的概率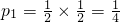 ,
,
“两枚都是反面朝上”的概率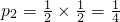 ,
,
“恰好一枚硬币正面朝上”的概率= .故①不正确;
.故①不正确;
②∵样本9,10,11,x,y的平均数是10,
∴x+y=20.
∵标准差是 ,
,
∴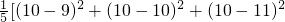 +(10-x)2+(10-y)2]=2,
+(10-x)2+(10-y)2]=2,
∴x2+y2-20(x+y)+200=8,
∴xy=96.故②成立;
③已知两相关变量x,y之间的一组数据如下:(0,8),(1,2),(2,6),(3,4),则线性回归方程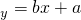 所表示的直线必恒经过点(1.5,5).故③不成立;
所表示的直线必恒经过点(1.5,5).故③不成立;
④在AB上取M使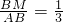 ,即
,即 ,
,
过M作MN‖BC交AC于N,
∴△ABC∽△AMN,
∴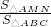 =
= =(
=( )2=
)2= ,
,
∵S在△ANM中不满足要求,S在梯形MNCB中满足要求,
∴概率=
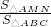 =
= .故④成立.
.故④成立.
故答案为:②④.
点评:本题考查命题的真假判断和应用,解题时要注意极差、方差和标准差的合理运用.
分析:①抛掷两枚硬币,出现“两枚都是正面朝上”的概率=“两枚都是反面朝上”的概率=
 ,“恰好一枚硬币正面朝上”的概率=
,“恰好一枚硬币正面朝上”的概率= .故①不正确;②由样本9,10,11,x,y的平均数是10,知x+y=20.由标准差是
.故①不正确;②由样本9,10,11,x,y的平均数是10,知x+y=20.由标准差是 ,知x2+y2-20(x+y)+200=8,所以xy=96.故②成立;③线性回归方程
,知x2+y2-20(x+y)+200=8,所以xy=96.故②成立;③线性回归方程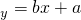 所表示的直线必恒经过点(1.5,5).故③不成立;④在AB上取M使
所表示的直线必恒经过点(1.5,5).故③不成立;④在AB上取M使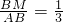 ,即
,即 ,过M作MN‖BC交AC于N,△ABC∽△AMN,由S在△ANM中不满足要求,S在梯形MNCB中满足要求,知概率=
,过M作MN‖BC交AC于N,△ABC∽△AMN,由S在△ANM中不满足要求,S在梯形MNCB中满足要求,知概率=
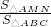 =
= .故④成立.
.故④成立.解答:①抛掷两枚硬币,出现“两枚都是正面朝上”的概率
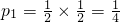 ,
,“两枚都是反面朝上”的概率
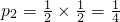 ,
,“恰好一枚硬币正面朝上”的概率=
 .故①不正确;
.故①不正确;②∵样本9,10,11,x,y的平均数是10,
∴x+y=20.
∵标准差是
 ,
,∴
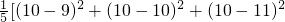 +(10-x)2+(10-y)2]=2,
+(10-x)2+(10-y)2]=2,∴x2+y2-20(x+y)+200=8,
∴xy=96.故②成立;
③已知两相关变量x,y之间的一组数据如下:(0,8),(1,2),(2,6),(3,4),则线性回归方程
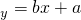 所表示的直线必恒经过点(1.5,5).故③不成立;
所表示的直线必恒经过点(1.5,5).故③不成立;④在AB上取M使
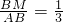 ,即
,即 ,
,过M作MN‖BC交AC于N,
∴△ABC∽△AMN,
∴
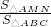 =
= =(
=( )2=
)2= ,
,∵S在△ANM中不满足要求,S在梯形MNCB中满足要求,
∴概率=

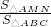 =
= .故④成立.
.故④成立.故答案为:②④.
点评:本题考查命题的真假判断和应用,解题时要注意极差、方差和标准差的合理运用.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目