Question

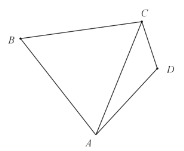
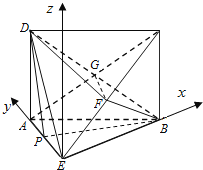
【题目】如图，在四棱锥E﹣ABCD中，底面ABCD为矩形，平面ABCD⊥平面ABE，∠AEB＝90°，BE＝BC，F为CE的中点，

（1）求证：AE∥平面BDF；

（2）求证：平面BDF⊥平面ACE；

（3）2AE＝EB，在线段AE上找一点P，使得二面角P﹣DB﹣F的余弦值为，求P的位置．

Answer 1

【答案】（1）见解析（2）见解析（3）P在E处．

【解析】

（1）通过证明FG∥AE即可证明；

（2）通过证明BF⊥平面ACE，即可证得面面垂直；

（3）建立空间直角坐标系，利用两个半平面法向量关系求解.

证明：（1）设AC∩BD＝G，连接FG，易知G是AC的中点，

∵F是EC中点．

∴在△ACE中，FG∥AE，

∵AE平面BFD，FG平面BFD，

∴AE∥平面BFD．

（2）∵平面ABCD⊥平面ABE，BC⊥AB，

平面ABCD∩平面ABE＝AB，

∴BC⊥平面ABE，又∵AE平面ABE，

∴BC⊥AE，

又∵AE⊥BE，BC∩BE＝B，

∴AE⊥平面BCE，即AE⊥BF，

在△BCE中，BE＝CB，F为CE的中点，

∴BF⊥CE，AE∩CE＝E，

∴BF⊥平面ACE，

又BF平面BDF，

∴平面BDF⊥平面ACE．

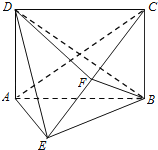
（3）如图建立坐标系，设AE＝1，

则B（2，0，0），D（0，1，2），C（2，0，2），F（1，0，1），

设P（0，a，0），，，

设平面BDF的法向量为，且，

则由⊥得﹣2x1+y1+2z1＝0，

由⊥得﹣x1+z1＝0，

令z1＝1得x1＝1，y1＝0，从而

设平面BDP的法向量为，且，则

由⊥得﹣2x2+y2+2z2＝0，

由⊥得2x2﹣ay2＝0，

令y2＝2得x2＝a，z2＝a﹣1，从而，

，

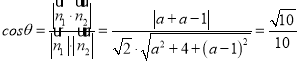解得a＝0或a＝1（舍）

即P在E处．