题目内容
a1,a2,…,an是1,2,…,n的一个排列.证明
+
+…+
≤
+
+…+
.
证明:∵(a1+1)(a2+1)…(an-1+1)≥(1+1)(2+1)…(n-1+1)=a1a2…an,?
则++…++++…+
=
+
+…+
+
+…+
=
+
+…+
≥n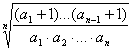
≥n.?
由n≤(
+
+…+
)+(1+
+…+
),?
∴
+…+
≥
+…+
.
练习册系列答案
阅读快车系列答案
相关题目
阅读快车系列答案题目内容
a1,a2,…,an是1,2,…,n的一个排列.证明++…+≤++…+.
证明:∵(a1+1)(a2+1)…(an-1+1)≥(1+1)(2+1)…(n-1+1)=a1a2…an,?
则++…++++…+
=++…+++…+
=++…+
≥n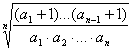
≥n.?
由n≤(++…+)+(1++…+),?
∴+…+≥+…+.
阅读快车系列答案