[题目]函数f(x)=ex(x﹣aex) 恰有两个极值点x1 . x2(x1＜x2).则a的取值范围是．题目和参考答案——青夏教育精英家教网—

题目内容

【题目】函数f（x）=ex（x﹣aex）恰有两个极值点x1 ， x2（x1＜x2），则a的取值范围是．

【答案】（0, ）
【解析】解：∵函数f（x）=ex（x﹣aex），求导，f′（x）=（x+1﹣2aex）ex，

由于函数f（x）的两个极值点为x1，x2，

即x1，x2是方程f′（x）=0的两不等实根，

即方程x+1﹣2aex=0，且a≠0， =ex；

设y1= （a≠0），y2=ex，

在同一坐标系内画出这两个函数的图象，

如图所示：

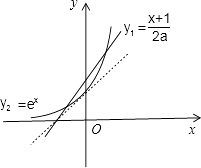
要使这两个函数有2个不同的交点，应满足，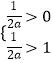

解得：0＜a＜，

∴a的取值范围是（0，），

所以答案是：（0，）．

【考点精析】掌握函数的极值与导数是解答本题的根本，需要知道求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值．

练习册系列答案

相关题目

【题目】在直角坐标系xOy中，直线l1的参数方程为，（t为参数），直线l2的参数方程为，（m为参数）．设l1与l2的交点为P，当k变化时，P的轨迹为曲线C．
（1）写出C的普通方程；
（2）以坐标原点为极点，x轴正半轴为极轴建立极坐标系，设l3：ρ（cosθ+sinθ）﹣ =0，M为l3与C的交点，求M的极径．

【题目】如图，在直角梯形ABCD中，BC⊥DC，AE⊥DC，M，N分别是AD，BE的中点，将三角形ADE沿AE折起，则下列说法正确的是________(填序号)．

①不论D折至何位置(不在平面ABC内)，都有MN∥平面DEC；②不论D折至何位置，都有MN⊥AE；③不论D折至何位置(不在平面ABC内)，都有MN∥AB；④在折起过程中，一定存在某个位置，使EC⊥AD.

【题目】已知函数f（x）= x2﹣alnx（a∈R）
（1）若函数f（x）在x=2处的切线方程为y=x+b，求a，b的值；
（2）讨论方程f（x）=0解的个数，并说明理由．

【题目】如图，四棱锥P－ABCD中，PA⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，PA＝BC＝4，M为线段AD上一点，AM＝2MD，N为PC的中点．

(1)证明MN∥平面PAB；

(2)求四面体N－BCM的体积．

【题目】定义：如果函数y=f（x）在定义域内给定区间[a，b]上存在x0（a＜x0＜b），满足f（x0）= ，则称函数y=f（x）是[a，b]上的“平均值函数”，x0是它的一个均值点．例如y=|x|是[﹣2，2]上的平均值函数，0就是它的均值点．若函数f（x）=x2﹣mx﹣1是[﹣1，1]上的“平均值函数”，则实数m的取值范围是．

【题目】如图，四棱锥S﹣ABCD中，AB∥CD，BC⊥CD，侧面SAB为等边三角形．AB=BC=2，CD=SD=1．
（1）证明：SD⊥平面SAB
（2）求AB与平面SBC所成角的正弦值．

【题目】已知函数g（x）=ax2-2ax+1+b（a>0）在区间[2，4]上的最大值为9，最小值为1，记f（x）=g（|x|）。

（1）求实数a，b的值；

（2）若不等式f（2k）>1成立，求实数k的取值范围；

（3）定义在[p，q]上的函数（x），设p=x0<x1<…<xi-1<xi<…<xn=q，x1，x2，…，xn-l将区间[p，q]任意划分成n个小区间，如果存在一个常数M>0，使得和式恒成立，则称函数（x）为在[p，q]上的有界变差函数。试判断函数f（x）是否为在[0，4]上的有界变差函数?若是，求M的最小值；若不是，请说明理由。

【题目】某市居民自来水收费标准如下：每户每月用水不超过4吨时，每吨为1.80元，当用水超过4吨时，超过部分每吨3.00元．某月甲、乙两户共交水费y元，已知甲、乙两用户该月用水量分别为5x，3x吨．（Ⅰ）若x=1，求该月甲、乙两户的水费；
（Ⅱ）求y关于x的函数；
（Ⅲ）若甲、乙两户该月共交水费26.4元，分别求出甲、乙两户该月的用水量．

试题分类