题目内容
已知△ABC三个顶点的坐标分别是A(0,2),B(1,1),C(1,3).若△ABC在一个切变变换T作用下变为△A1B1C1,其中B(1,1)在变换T作用下变为点B1(1,-1).
(1)求切变变换T所对应的矩阵M;
(2)将△A1B1C1绕原点O按顺时针方向旋转30°后得到△A2B2C2.求△A2B2C2的面积.
(1)求切变变换T所对应的矩阵M;
(2)将△A1B1C1绕原点O按顺时针方向旋转30°后得到△A2B2C2.求△A2B2C2的面积.
考点:变换、矩阵的相等
专题:计算题
分析:(1)设M=
,由B(1,1)在变换T作用下变为点B1(1,-1)可得:
•
=
,即
,解得矩阵M;
(2)将△A1B1C1绕原点O按顺时针方向旋转30°后得到△A2B2C2.根据旋转变换不改变图形的形状,可得变换前后三角形面积不变,进而得到答案.
|
|
|
|
|
(2)将△A1B1C1绕原点O按顺时针方向旋转30°后得到△A2B2C2.根据旋转变换不改变图形的形状,可得变换前后三角形面积不变,进而得到答案.
解答:
解:(1)设M=
,
∵B(1,1)在变换T作用下变为点B1(1,-1).
∴
•
=
,
即
,
解得:b=-2,c=0,
∴M=
…(4分)
(2)因为△ABC在变换T作用下变为△A1B1C1,
三个顶点的坐标分别是(0,2),(1,-1)和(1,1),其面积为1.
而旋转变换不改变图形的形状,所以其面积不变,依然为1.
所以,△△A2B2C2的面积为1.…(10分)
|
∵B(1,1)在变换T作用下变为点B1(1,-1).
∴
|
|
|
即
|
解得:b=-2,c=0,
∴M=
|
(2)因为△ABC在变换T作用下变为△A1B1C1,
三个顶点的坐标分别是(0,2),(1,-1)和(1,1),其面积为1.
而旋转变换不改变图形的形状,所以其面积不变,依然为1.
所以,△△A2B2C2的面积为1.…(10分)
点评:本题考查变换与矩阵的相等,着重考查了矩阵的乘法法则和矩阵变换的含义等知识,属于较基础题.

练习册系列答案
相关题目


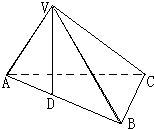 如图,三棱锥V-ABC中,△VAB是边长为2的正三角形,点V在平面ABC上的射影D在AB边上,△ABC是以B为直角顶点的等腰直角三角形.
如图,三棱锥V-ABC中,△VAB是边长为2的正三角形,点V在平面ABC上的射影D在AB边上,△ABC是以B为直角顶点的等腰直角三角形.