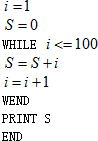题目内容
17.函数$y={(\frac{1}{3})^{cosx}}$的单调递增区间为[2kπ,2kπ+π],k∈Z.分析 设t=x2-2x,利用换元法结合复合函数单调性之间的关系进行求解即可.
解答 解:设t=cosx,
则y=($\frac{1}{3}$)t为减函数,
要求函数$y={(\frac{1}{3})^{cosx}}$的单调增区间,即求函数t=cosx的单调递减区间,
∵t=cosx的单调递减区间是[2kπ,2kπ+π],k∈Z,
∴函数$y={(\frac{1}{3})^{cosx}}$的单调递增区间为[2kπ,2kπ+π],k∈Z,
故答案为:[2kπ,2kπ+π],k∈Z,
点评 本题主要考查函数单调区间的求解,利用换元法结合复合函数单调性之间的关系是解决本题的关键.

练习册系列答案
相关题目
2.已知复数Z=$\frac{1-\sqrt{3}i}{(\sqrt{3}+i)^{2}}$,$\overline{Z}$是Z的共轭复数,则Z•$\overline{Z}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | 2 | D. | 4 |
9.下列函数中,为偶函数的是( )
| A. | f(x)=x | B. | f(x)=sinx | C. | f(x)=$\frac{1}{x}$ | D. | f(x)=x2 |
7.函数y=sinx的图象( )
| A. | 关于点$({\frac{π}{2},1})$对称 | B. | 关于直线x=π对称 | C. | 关于点(π,0)对称 | D. | 关于y轴对称 |