题目内容
直线l过直线x + y-2 = 0和直线x-y + 4 = 0的交点,且与直线3x-2y + 4 = 0平行,求直线l的方程.
解法一:联立方程: 解得
解得  ,即直线l过点(-1,3),
,即直线l过点(-1,3),
∵直线l的斜率为 ,∴直线l的方程为:y-3 =
,∴直线l的方程为:y-3 =  (x + 1) 即3x-2y + 9 = 0.
(x + 1) 即3x-2y + 9 = 0.
解法二:∵直线x + y-2 = 0不与3x-2y + 4 = 0平行 ∴可设直线l的方程为:x-y + 4 + λ(x + y-2)= 0
整理得:(1 + λ)x + (λ-1)y + 4-2λ = 0 ∵直线l与直线3x-2y + 4 = 0平行
∴ 解得λ =
解得λ = 
∴直线l的方程为: x-
x-  y +
y +  = 0 即3x-2y + 9 = 0
= 0 即3x-2y + 9 = 0

练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
 ”是“函数
”是“函数 在区间
在区间 内单调递增”的 ( )
内单调递增”的 ( )
 中,
中, 、
、 是棱
是棱 上互异的两点,
上互异的两点,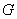 、
、 是棱
是棱 上互异的两点,由图可知
上互异的两点,由图可知 与
与 互为异面直线; ②
互为异面直线; ②  分别与
分别与 、
、 互为异面直线;
互为异面直线; 与
与 ①③
①③  ②④
②④  ①②④
①②④  ①②③④
①②③④
 轴上的截距为
轴上的截距为 的直线方程是( )
的直线方程是( ) B.
B.  C.
C.  D.
D. 
 ,则此球的表面积是 ( )
,则此球的表面积是 ( ) D.
D.
 是虚数单位,复数
是虚数单位,复数 = ( )
= ( ) B.
B. C.
C. D.
D.
 ,则
,则 ,均有
,均有 ;
; 是直线
是直线 与直线
与直线 互相垂直的充要条件;
互相垂直的充要条件; =1.23x+0.08
=1.23x+0.08 ,则满足
,则满足 的概率为
的概率为 .
. 与
与 所围成图形的面积是
所围成图形的面积是
 满足
满足 则
则 ( )
( ) 的解集是 .
的解集是 .